题目内容
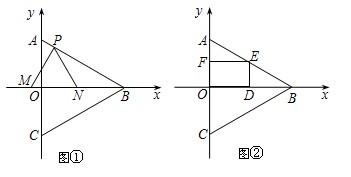
 如图所示,矩形ABCD中,AB=2,BC=3,P为BC边上与BC两点不重合的任意一点.设PA=x,D到PA的距离为y,则y与x的函数关系式为________,自变量的取值范围是________.
如图所示,矩形ABCD中,AB=2,BC=3,P为BC边上与BC两点不重合的任意一点.设PA=x,D到PA的距离为y,则y与x的函数关系式为________,自变量的取值范围是________.
y=

分析:把已知的线段用含x、y的代数式表示出来,转化到两个三角形中,易证其相似,从而得出关系式,进而求出x的取值范围.
解答:∵四边形ABCD是矩形,
∴AD∥BC,∠B=90°,
∴∠DAE=∠APB,
∵DE⊥AP,∴∠AED=90°,
∴∠B=∠AED=90°,
∴△ABP∽△DEA;
∴ ,
,
即: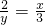 ,
,
∴y= ,
,
故答案为:y= ,
,
∵AP为直角三角形ABP的斜边,AB=2,
∴AP>2,即x>2,
∵当点P移动到点C时AP最长,
∴AP=x= =
= =
= ,
,
∵AP< ,
,
∴2<x< ,
,
故答案为:2<x< .
.
点评:此题主要利用了相似三角形的性质,利用性质建立已知和未知之间的联系是关键,根据图形化到相应的部分中,运用相关知识解决.


分析:把已知的线段用含x、y的代数式表示出来,转化到两个三角形中,易证其相似,从而得出关系式,进而求出x的取值范围.
解答:∵四边形ABCD是矩形,
∴AD∥BC,∠B=90°,
∴∠DAE=∠APB,

∵DE⊥AP,∴∠AED=90°,
∴∠B=∠AED=90°,
∴△ABP∽△DEA;
∴
 ,
,即:
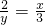 ,
,∴y=
 ,
,故答案为:y=
 ,
,∵AP为直角三角形ABP的斜边,AB=2,
∴AP>2,即x>2,
∵当点P移动到点C时AP最长,
∴AP=x=
 =
= =
= ,
,∵AP<
 ,
,∴2<x<
 ,
,故答案为:2<x<
 .
.点评:此题主要利用了相似三角形的性质,利用性质建立已知和未知之间的联系是关键,根据图形化到相应的部分中,运用相关知识解决.

练习册系列答案
相关题目
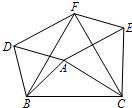 18、如图所示,在△ABC中,分别以AB、AC、BC为边在BC的同侧作等边△ABD,等边△ACE、等边△BCF.
18、如图所示,在△ABC中,分别以AB、AC、BC为边在BC的同侧作等边△ABD,等边△ACE、等边△BCF.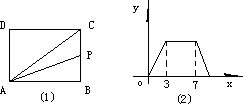
 边在△AOB内部作如图所示的矩形ODEF,点E在线段AB上.
边在△AOB内部作如图所示的矩形ODEF,点E在线段AB上. (2012•邵阳)如图所示,在△ABC中,AB=AC,∠A<90°,边BC、CA、AB的中点分别是D、E、F,则四边形AFDE是( )
(2012•邵阳)如图所示,在△ABC中,AB=AC,∠A<90°,边BC、CA、AB的中点分别是D、E、F,则四边形AFDE是( )