题目内容
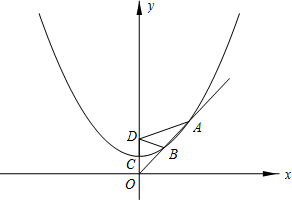
已知抛物线的顶点是C(0,a) (a>0,a为常数),并经过点(2a,2a),点D(0,2a)为一定点。
(1)求含有常数a的抛物线的解析式;
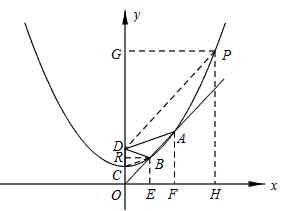
(2)设点P是抛物线任意一点,过P作PH⊥x轴,垂足是H,求证:PD=PH;
(3)设过原点O的直线l与抛物线在第一象限相交于A、B两点,若DA=2DB,且S△ABD=4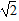 ,求a的值。
,求a的值。
(1)求含有常数a的抛物线的解析式;
(2)设点P是抛物线任意一点,过P作PH⊥x轴,垂足是H,求证:PD=PH;
(3)设过原点O的直线l与抛物线在第一象限相交于A、B两点,若DA=2DB,且S△ABD=4
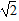 ,求a的值。
,求a的值。 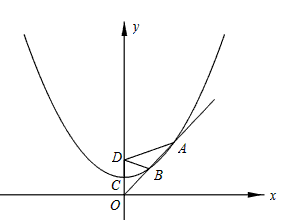
| 解:(1)设抛物线的解析式为y=kx2+a, ∵点D(2a,2a)在抛物线上, 4a2k+a=2a, ∴k= 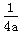 , ,∴抛物线的解析式为y= 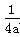 x2+a; x2+a; |
|
| (2)设抛物线上一点P(x,y),过P作PH⊥x轴,PG⊥y轴, 在Rt△GDP中,由勾股定理得:PD2=DG2+PG2=(y-2a)2+x2=y2-4ay+4a2+x2, ∵y= 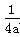 x2+a x2+a ∴x2= 4a×(y-a)=4ay-4a2, ∴PD2=y2-4ay+4a2+4ay-4a2=y2=PH2, ∴PD=PH。 |
|
|
(3)过B点BE⊥x轴,AF⊥x轴, |
 |

练习册系列答案
相关题目
 =
= =BE=DB,
=BE=DB, =
= ,
,  ,又点B在抛物线上,
,又点B在抛物线上,  x2+a,
x2+a, a,
a, a,
a, )
) 
 ×2a×
×2a× a=4
a=4