题目内容
15、已知ab=6，a+b=5，则a3b+2a2b2+ab3的值为
150
．分析：首先将原式因式分解得出ab（a+b）2；再利用ab=6，a+b=5，求出即可．
解答：解：∵a3b+2a2b2+ab3，
=ab（a2+b2+2ab），
=ab（a+b）2；
∵a+b=5，
∴（a+b）2=25，
∵ab=6，
∴原式=6×25=150．
故答案为：150．
=ab（a2+b2+2ab），
=ab（a+b）2；
∵a+b=5，
∴（a+b）2=25，
∵ab=6，
∴原式=6×25=150．
故答案为：150．
点评：此题考查了因式分解法的应用，熟记公式结构正确将原式分解因式是解题的关键．
练习册系列答案
名校练考卷期末冲刺卷系列答案
相关题目
10、如图，已知AB是⊙O的直径，C是⊙O外一点，CA、CB交⊙O分别于D、E点，且AB=1，则cos∠C=（ ）
如图：折叠长方形ABCD（四个角都是直角，对边相等）的一边AD，点D落在BC边的F处，已知AB=8cm，BC=10cm，则EC=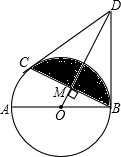
如图，已知AB为⊙O的直径，BD为⊙O的切线，过点B的弦BC⊥OD交⊙O于点C，垂足为M．