题目内容
在同一平面上，已知OA⊥OC，OB⊥OD，若∠BOC=45°，则∠AOD=
135°或45°
135°或45°
．分析：讨论：根据垂线的性质得到∠AOC=90°，∠BOD=90°．如图1，根据等角的余角相等即可得到∠AOD．如图2，利用周角为360°即可计算出∠AOD；
解答：
解：如图1，∵OA⊥OC，OB⊥OD，
∴∠AOC=90°，∠BOD=90°．
∵∠BOC=45°，
∴∠COD=90°-∠BOC=45°，
∴∠AOD=∠AOC+∠COD=135°；
如图2，∵OA⊥OC，OB⊥OD，
∴∠AOC=90°，∠BOD=90°，
∵∠BOC=45°，
∴∠AOD=360°-90°-45°-90°=45°．
综上所述，∠AOD=135°或45°．
故答案是：135°或45°．
解：如图1，∵OA⊥OC，OB⊥OD，∴∠AOC=90°，∠BOD=90°．
∵∠BOC=45°，
∴∠COD=90°-∠BOC=45°，
∴∠AOD=∠AOC+∠COD=135°；
如图2，∵OA⊥OC，OB⊥OD，
∴∠AOC=90°，∠BOD=90°，
∵∠BOC=45°，
∴∠AOD=360°-90°-45°-90°=45°．
综上所述，∠AOD=135°或45°．
故答案是：135°或45°．
点评：本题考查了垂线的性质：两直线垂直，则它们相交所成的角为90°．也考查了周角的定义以及等角的余角相等．
练习册系列答案
相关题目
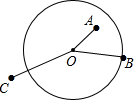如图，设⊙O的半径为r，A点在圆内，OA________r；B点在圆上，OB________r；C点在圆外，OC________r．反之，在同一平面上，已知⊙O的半径为r和A，B，C三点：若OA＞r，则A点在圆________；若OB＜r，则B点在圆________；若OC=r，则C点在圆________．