题目内容
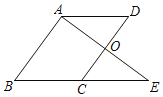
【题目】如图,矩形ABCD中,BC=8,点F是AB边上一点(不与点B重合)△BCF的外接圆交对角线BD于点E,连结CF交BD于点G.
(1)求证:∠ECG=∠BDC.
(2)当AB=6时,在点F的整个运动过程中.
①若BF=2![]() 时,求CE的长.
时,求CE的长.
②当△CEG为等腰三角形时,求所有满足条件的BE的长.
(3)过点E作△BCF外接圆的切线交AD于点P.若PE∥CF且CF=6PE,记△DEP的面积为S1,△CDE的面积为S2,请直接写出![]() 的值.
的值.
【答案】(1)详见解析;(2)①![]() ;②当BE为10,
;②当BE为10,![]() 或
或![]() 时,△CEG为等腰三角形;(3)
时,△CEG为等腰三角形;(3)![]() .
.
【解析】
(1)根据平行线的性质得出∠ABD=∠BDC,根据圆周角定理得出∠ABD=∠ECG,即可证得结论;
(2)根据勾股定理求得BD=10,
①连接EF,根据圆周角定理得出∠CEF=∠BCD=90°,∠EFC=∠CBD.即可得出sin∠EFC=sin∠CBD,得出![]() ,根据勾股定理得到CF=
,根据勾股定理得到CF=![]() ,即可求得CE=
,即可求得CE=![]() ;
;
②分三种情况讨论求得:
当EG=CG时,根据等腰三角形的性质和圆周角定理即可得到∠GEC=∠GCE=∠ABD=∠BDC,从而证得E、D重合,即可得到BE=BD=10;
当GE=CE时,过点C作CH⊥BD于点H,即可得到∠EGC=∠ECG=∠ABD=∠GDC,得到CG=CD=6.根据三角形面积公式求得CH=![]() ,即可根据勾股定理求得GH,进而求得HE,即可求得BE=BH+HE=
,即可根据勾股定理求得GH,进而求得HE,即可求得BE=BH+HE=![]() ;
;
当CG=CE时,过点E作EM⊥CG于点M,由tan∠ECM=![]() .设EM=4k,则CM=3k,CG=CE=5k.得出GM=2k,tan∠GEM=
.设EM=4k,则CM=3k,CG=CE=5k.得出GM=2k,tan∠GEM=![]() ,即可得到tan∠GCH=
,即可得到tan∠GCH=![]() =
=![]() .求得HE=GH=
.求得HE=GH=![]() ,即可得到BE=BH+HE=
,即可得到BE=BH+HE=![]() ;
;
(3)连接OE、EF、AE、EF,先根据切线的性质和垂直平分线的性质得出EF=CE,进而证得四边形ABCD是正方形,进一步证得△ADE≌△CDE,通过证得△EHP∽△FBC,得出EH=![]() BF,即可求得BF=6,根据勾股定理求得CF=10,得出PE=
BF,即可求得BF=6,根据勾股定理求得CF=10,得出PE=![]() ,根据勾股定理求得PH,进而求得PD,然后根据三角形面积公式即可求得结果.
,根据勾股定理求得PH,进而求得PD,然后根据三角形面积公式即可求得结果.
(1)证明:∵AB∥CD.
∴∠ABD=∠BDC,
∵∠ABD=∠ECG,
∴∠ECG=∠BDC.
(2)解:①∵AB=CD=6,AD=BC=8,
∴BD=![]() =10,
=10,
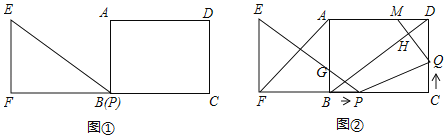
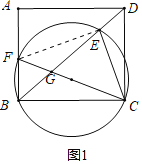
如图1,连结EF,则∠CEF=∠BCD=90°,
∵∠EFC=∠CBD.
∴sin∠EFC=sin∠CBD,
∴![]()
∴CF=![]() =
=![]() ,
,
∴CE=![]() .
.
②Ⅰ、当EG=CG时,∠GEC=∠GCE=∠ABD=∠BDC.
∴E与D重合,
∴BE=BD=10.
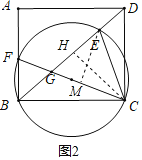
Ⅱ、如图2,当GE=CE时,过点C作CH⊥BD于点H,
∴∠EGC=∠ECG=∠ABD=∠GDC,
∴CG=CD=6.
∵CH=![]() ,
,
∴GH=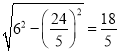 ,
,
在Rt△CEH中,设HE=x,则x2+(![]() )2=(x+
)2=(x+![]() )2
)2
解得x=![]() ,
,
∴BE=BH+HE=![]() +
+![]() =
=![]() ;
;
Ⅲ、如图2,当CG=CE时,
过点E作EM⊥CG于点M.
∵tan∠ECM=![]() .
.
设EM=4k,则CM=3k,CG=CE=5k.
∴GM=2k,tan∠GEM=![]() ,
,
∴tan∠GCH=![]() =tan∠GEM=
=tan∠GEM=![]() .
.
∴HE=GH=![]() ,
,
∴BE=BH+HE=![]() ,
,
综上所述,当BE为10,![]() 或
或![]() 时,△CEG为等腰三角形;
时,△CEG为等腰三角形;
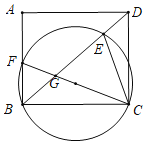
(3)解:∵∠ABC=90°,
∴FC是△BCF的外接圆的直径,设圆心为O,
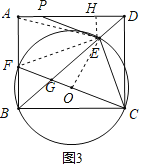
如图3,连接OE、EF、AE、EF,
∵PE是切线,
∴OE⊥PE,
∵PE∥CF,
∴OE⊥CF,
∵OC=OF,
∴CE=EF,
∴△CEF是等腰直角三角形,
∴∠ECF=45°,EF=![]() FC,
FC,
∴∠ABD=∠ECF=45°,
∴∠ADB=∠BDC=45°,
∴AB=AD=8,
∴四边形ABCD是正方形,
∵PE∥FC,
∴∠EGF=∠PED,
∴∠BGC=∠PED,
∴∠BCF=∠DPE,
作EH⊥AD于H,则EH=DH,
∵∠EHP=∠FBC=90°,
∴△EHP∽△FBC,
∴![]() ,
,
∴EH=![]() BF,
BF,
∵AD=CD,∠ADE=∠CDE,
∴△ADE≌△CDE,
∴AE=CE,
∴AE=EF,
∴AF=2EH=![]() BF,
BF,
∴![]() BF+BF=8,
BF+BF=8,
∴BF=6,
∴EH=DH=1,CF=![]() =10,
=10,
∴PE=![]() FC=
FC=![]() ,
,
∴PH=![]() ,
,
∴PD=![]() ,
,
∴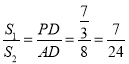 .
.

 名校课堂系列答案
名校课堂系列答案