题目内容
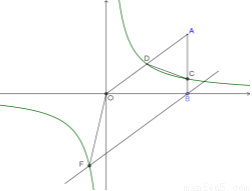
如图，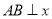 
轴于点
， 
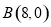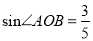，反比例函数
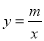与OA、AB分别相交于点D、C，且点D为OA的中点，
（1）求反比例函数的解析式
（2）过点B的直线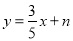
与反比例函数
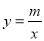图象交于第三象限内一点F，求四边形
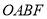的面积
练习册系列答案
名校课堂系列答案
相关题目
名校课堂系列答案题目内容
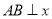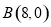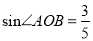如图， 轴于点， ，反比例函数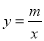与OA、AB分别相交于点D、C，且点D为OA的中点，
（1）求反比例函数的解析式
（2）过点B的直线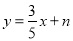与反比例函数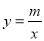图象交于第三象限内一点F，求四边形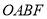的面积
名校课堂系列答案
为矩形
的边
上一点，将矩形
沿
折叠的一边，使点
落在
边的点
处．若折痕
，则
的长为___________。
天，红星厂每天可加工
件产品，巨星厂每天可加工
件产品，公司需付红星厂每天加工费
元，巨星厂每天加工费
元．
）这个公司要加工多少件新产品？
）在加工过程中，公司需令派一名工程师每天到厂家进行指导，并负担每天
元的午餐补助费，公司制定的方案中，选择一种既省钱又省时的加工方案．