Question

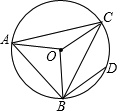如图，△ABC是⊙O的内接三角形，点D是弧BC的中点，已知∠AOB=100°，∠COB=120°，则∠ABD的度数是

 

．

Answer 1

考点：圆周角定理

专题：计算题

分析：连结OD，易得∠OAB=∠OBA，根据三角形内角和定理得∠OBA=

1

2

（180°-∠AOB）=40°，由点D是弧BC的中点得∠BOD=∠COD=

1

2

∠BOC=60°，所以∠OBD=60°，然后利用∠ABD=∠OBA+∠OBD进行计算．

解答：解：连结OD，如图，
∵OA=OB，
∴∠OAB=∠OBA，
∴∠OBA=

1

2

（180°-∠AOB）=

1

2

（180°-100°）=40°，
∵点D是弧BC的中点，
∴∠BOD=∠COD=

1

2

∠BOC=

1

2

×120°=60°，
∴∠OBD=60°，
∴∠ABD=∠OBA+∠OBD=40°+60°=100°．
故答案为100°．

点评：本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．