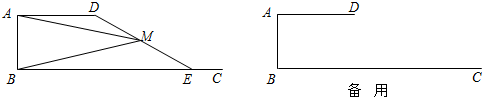题目内容
 如图,直角梯形ABME中,∠M=90゜,BM∥AE,以AB为直径的⊙O与EM切于点C,连BE,若AE=6,AB=10,则tan∠BEM的值为
如图,直角梯形ABME中,∠M=90゜,BM∥AE,以AB为直径的⊙O与EM切于点C,连BE,若AE=6,AB=10,则tan∠BEM的值为
- A.

- B.

- C.

- D.

D
分析:连接OC,过B作BN⊥AE于N,求出OC是梯形AEMB的中位线,求出BM,证矩形ENBM,得出EM=BN,EN=BM,求出BN,解直角三角形求出即可.
解答:
连接OC,过B作BN⊥AE于N,
∵∠M=90°,AE∥BM,
∴∠M=∠NEM=∠BNE=90°,
∴四边形ENBM是矩形,
∴EM=BN,EN=BM,
∵⊙O切EM于C,
∴OC⊥EM,
∴BM∥OC∥AE,
∵AO=OB,
∴EC=CM,
∴OC=5= (AE+BM),
(AE+BM),
∵OC= AB=5,AE=6,
AB=5,AE=6,
∴BM=4=EN,
在Rt△ANB中,AN=6-4=2,AB=10,由勾股定理得:EM=BN= =4
=4 ,
,
在Rt△BME中,tan∠BEM= =
=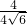 =
= ,
,
故选D.
点评:本题考查了梯形的中位线,切线性质,解直角三角形,勾股定理,矩形的性质和判定的应用,主要考查学生综合运用性质进行推理和计算的能力.
分析:连接OC,过B作BN⊥AE于N,求出OC是梯形AEMB的中位线,求出BM,证矩形ENBM,得出EM=BN,EN=BM,求出BN,解直角三角形求出即可.
解答:

连接OC,过B作BN⊥AE于N,
∵∠M=90°,AE∥BM,
∴∠M=∠NEM=∠BNE=90°,
∴四边形ENBM是矩形,
∴EM=BN,EN=BM,
∵⊙O切EM于C,
∴OC⊥EM,
∴BM∥OC∥AE,
∵AO=OB,
∴EC=CM,
∴OC=5=
 (AE+BM),
(AE+BM),∵OC=
 AB=5,AE=6,
AB=5,AE=6,∴BM=4=EN,
在Rt△ANB中,AN=6-4=2,AB=10,由勾股定理得:EM=BN=
 =4
=4 ,
,在Rt△BME中,tan∠BEM=
 =
=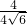 =
= ,
,故选D.
点评:本题考查了梯形的中位线,切线性质,解直角三角形,勾股定理,矩形的性质和判定的应用,主要考查学生综合运用性质进行推理和计算的能力.

练习册系列答案
相关题目
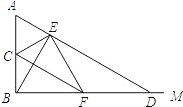 ,连接AD,作BE⊥AD,垂足为E,连接CE,过点E作EF⊥CE,交BD于F.
,连接AD,作BE⊥AD,垂足为E,连接CE,过点E作EF⊥CE,交BD于F.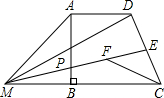 如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°.点E是DC的中点,过点E作DC的垂线交AB于点P,交CB的延长线于点M.点F在线段ME上,且满足CF=AD,MF=MA.则下列结论:①若∠MFC=130°,则∠MAB=40°;②∠MPB=90°-
如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°.点E是DC的中点,过点E作DC的垂线交AB于点P,交CB的延长线于点M.点F在线段ME上,且满足CF=AD,MF=MA.则下列结论:①若∠MFC=130°,则∠MAB=40°;②∠MPB=90°-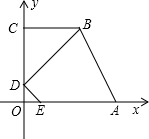 于点E.
于点E.  如图,在直角梯形ABCD中,AB=BC=4,M为腰BC上一点,且△ADM为等边三角形,则S△CDM:S△ABM=
如图,在直角梯形ABCD中,AB=BC=4,M为腰BC上一点,且△ADM为等边三角形,则S△CDM:S△ABM=