题目内容
 20、如图,一个直角三角形纸片的顶点A在∠MON的边OM上移动,移动过程中始终保持AB⊥ON于点B,AC⊥OM于点A.∠MON的角平分线OP分别交AB、AC于D、E两点.
20、如图,一个直角三角形纸片的顶点A在∠MON的边OM上移动,移动过程中始终保持AB⊥ON于点B,AC⊥OM于点A.∠MON的角平分线OP分别交AB、AC于D、E两点.(1)点A在移动的过程中,线段AD和AE有怎样的数量关系,并说明理由.
(2)点A在移动的过程中,若射线ON上始终存在一点F与点A关于OP所在的直线对称,判断并说明以A、D、F、E为顶点的四边形是怎样特殊的四边形?
(3)若∠MON=45°,猜想线段AC、AD、OC之间有怎样的数量关系,只写出结果即可.不用证明.
分析:(1)由AB⊥ON,AC⊥OM,根据两锐角互余,易证得∠AED=∠ADE,然后根据等角对等边的性质,即可得AD=AE;
(2)连接DF、EF,由点F与点A关于直线OP对称,E、D在OP上,可证得AE=FE,AD=FD,又由AD=AE,根据由四条边都相等的四边形是菱形,即可得四边形ADFE是菱形;
(3)首先过点E作EK⊥OC于K,AC⊥OM,∠MON的角平分线是OP,即可得AE=EK=AD,又由∠MON=45°,根据等腰直角三角形的性质,易得OA=AC=OK,,则可证得OC=AC+AD.
(2)连接DF、EF,由点F与点A关于直线OP对称,E、D在OP上,可证得AE=FE,AD=FD,又由AD=AE,根据由四条边都相等的四边形是菱形,即可得四边形ADFE是菱形;
(3)首先过点E作EK⊥OC于K,AC⊥OM,∠MON的角平分线是OP,即可得AE=EK=AD,又由∠MON=45°,根据等腰直角三角形的性质,易得OA=AC=OK,,则可证得OC=AC+AD.
解答:解:(1)AE=AD.
理由如下:
∵AB⊥ON,AC⊥OM,
∴∠AED=90°-∠MOP,∠ADE=∠ODB=90°-∠PON,
而∠MOP=∠NOP,
∴∠AED=∠ADE.
∴AD=AE.
(2)菱形.
理由:连接DF、EF,
∵点F与点A关于直线OP对称,E、D在OP上,
∴AE=FE,AD=FD.
由(1)得AE=AD,
∴AE=FE=AD=FD.
∴四边形ADFE是菱形;
(3)OC=AC+AD.
理由:过点E作EK⊥OC于K,
∵AC⊥OM,∠MON的角平分线是OP,
∴AE=EK=AD,OA=OK,
∵∠MON=45°,
∴∠ACO=∠AOC=45°,
∴OA=AC,∠KEC=∠KCE,
∴EK=CK,
∴CK=AE,
∴OC=OK+KC=OA+AE=AC+AD.
理由如下:
∵AB⊥ON,AC⊥OM,
∴∠AED=90°-∠MOP,∠ADE=∠ODB=90°-∠PON,
而∠MOP=∠NOP,
∴∠AED=∠ADE.
∴AD=AE.

(2)菱形.
理由:连接DF、EF,
∵点F与点A关于直线OP对称,E、D在OP上,
∴AE=FE,AD=FD.
由(1)得AE=AD,
∴AE=FE=AD=FD.
∴四边形ADFE是菱形;
(3)OC=AC+AD.
理由:过点E作EK⊥OC于K,
∵AC⊥OM,∠MON的角平分线是OP,
∴AE=EK=AD,OA=OK,
∵∠MON=45°,
∴∠ACO=∠AOC=45°,
∴OA=AC,∠KEC=∠KCE,
∴EK=CK,
∴CK=AE,
∴OC=OK+KC=OA+AE=AC+AD.
点评:此题考查了垂直的定义,菱形的判定,等腰三角形与等腰直角三角形的性质,以及角平分线的性质等知识.此题综合性较强,难度适中,解题的关键是注意数形结合思想的应用,注意辅助线的作法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
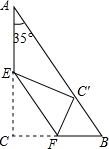 如图是一个直角三角形的纸片,将直角沿EF折叠,使C点落在AB边上,并且使∠EC′A=∠A,那么∠C′FE的度数是( )
如图是一个直角三角形的纸片,将直角沿EF折叠,使C点落在AB边上,并且使∠EC′A=∠A,那么∠C′FE的度数是( )| A、50° | B、45° | C、55° | D、70°第7题图 |
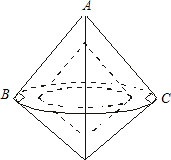 如图,一个直角三角形纸板,其两条直角边长分别为6cm和8cm,小明以纸板的斜边为旋转轴旋转这个三角形纸板形成如图所示的旋转体.请你帮小明推算出这个旋转体的全面积.(π取3.14)
如图,一个直角三角形纸板,其两条直角边长分别为6cm和8cm,小明以纸板的斜边为旋转轴旋转这个三角形纸板形成如图所示的旋转体.请你帮小明推算出这个旋转体的全面积.(π取3.14)
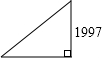 如图,一个直角三角形的三边长均为正整数,已知它的一条直角边的长恰是1997,那么另一条直角边的长为
如图,一个直角三角形的三边长均为正整数,已知它的一条直角边的长恰是1997,那么另一条直角边的长为 如图,一个直角三角形的三边长均为正整数,已知它的一条直角边的长恰是3,那么另一条直角边的长是
如图,一个直角三角形的三边长均为正整数,已知它的一条直角边的长恰是3,那么另一条直角边的长是