题目内容

设x≥0，y≥0，2x+y=6，则u=4x2+3xy+y2-6x-3y的最小值是（　　）
A．
27
2
B．18C．20D．不存在
由已知得：y=6-2x，代入u=4x2+3xy+y2-6x-3y，
整理得：u=2x2-6x+18，
而x≥0，y=6-2x≥0，则0≤x≤3，
u=2（x-
3
2
）2+
27
2
，
当x=0或x=3时，u取得最大值，umax=18，
当x=
3
2
时，u取得最小值，umin=
27
2
．
故选A．
练习册系列答案
相关题目
八年级某班级部分同学去植树，若每人平均植树7棵，还剩9棵，若每人平均植树9棵，则有1名同学植树的棵数不到8棵．若设同学人数为x人，下列各项能准确的求出同学人数与种植的树木的数量的是（　　）
A、7x+9-9（x-1）＞0
B、7x+9-9（x-1）＜8
C、
7x+9-9(x-1)≥0
7x+9-9(x-1)＜8
D、
7x+9-9(x-1)≥0
7x+9-9(x-1)≤8
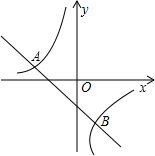精英家教网已知⊙O1的半径为R，周长为C．
（1）在⊙O1内任意作三条弦，其长分别是l1l2l3，求证：l1+l2+l3＜C；
（2）如图，在直角坐标系xOy中，设⊙O1的圆心为O1（R，R）．
①当直线l：y=x+b（b＞0）与⊙O1相切时，求b的值；
②当反比例函数y=
kx
（k＞0）的图象与⊙O1有两个交点时，求k的取值范围．
精英家教网如图，若反比例函数y=-
8x
与一次函数y=mx-2的图象都经过点A（a，2）
（1）求A点的坐标及一次函数的解析式；
（2）设一次函数与反比例函数图象的另一交点为B，求B点坐标，并利用函数图象写出使一次函数的值小于反比例函数的值的x的取值范围．
3、设x2-4x+2=0两根为x1，x2，则x1+x2-x1x2=（　　）
6、某县为发展教育事业，加强了对教育经费的投入，2007年投入3000万元，预计2009年投入5000万元．设教育经费的年平均增长率为x，根据题意，下面所列方程正确的是（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网