题目内容
如图，两同心圆的圆心为O，大圆的弦AB切小圆于P，两圆的半径分别为2和1，则弦长AB=______；若用阴影部分围成一个圆锥，则该圆锥的底面半径为______．（结果保留根号）．
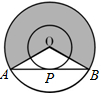
连接OP，则OP⊥AB，AB=2AP，
∴AB=2AP=2×
=2
，
∴sin∠AOP=
，
∴∠AOP=60°，
∴∠AOB=2∠AOP=120°，
∴优弧AB的长为
=
π，
∴圆锥的底面半径为
π÷2π=
．
∴AB=2AP=2×
| 22-12 |
| 3 |
∴sin∠AOP=
| ||
| 2 |
∴∠AOP=60°，
∴∠AOB=2∠AOP=120°，
∴优弧AB的长为
| 240π×2 |
| 180 |
| 8 |
| 3 |
∴圆锥的底面半径为
| 8 |
| 3 |
| 4 |
| 3 |
练习册系列答案
快乐5加2金卷系列答案
相关题目
