题目内容

已知直角三角形的两直角边长为3cm和4cm，则斜边上的中线长是cm，斜边上的高为cm．

$\text{[math]}$ $\text{[math]}$
分析：根据勾股定理先求出斜边，依据直角三角形中斜边上的中线等于斜边的一半求出中线长．再根据面积相等求出斜边上的高．
解答：根据勾股定理，斜边长为 $\text{[math]}$ =5cm，由于斜边上的中线长等于斜边的一半，故斜边上的中线长是 $\text{[math]}$ cm，根据面积相等，设斜边上的高为xcm，列方程得： $\text{[math]}$ •3•4= $\text{[math]}$ •5•x，解得x= $\text{[math]}$ cm．
故答案为 $\text{[math]}$ ， $\text{[math]}$ ．
点评：利用面积相等来解题，是解决直角三角形问题的常用的方法，可有效简化计算．

练习册系列答案

青苹果同步评价手册系列答案

初中英语知识集锦系列答案

小学语文词语手册吉林教育出版社系列答案

初中总复习中考精编系列答案

创新金卷毕业升学系列答案

创新课时训练系列答案

创新学案课时学练测系列答案

创新学习三级训练系列答案

创新与探究系列答案

达标测试卷系列答案

相关题目

学习过三角函数，我们知道在直角三角形中，一个锐角的大小与两条边长的比值相互唯一确定，因此边长与角的大小之间可以相互转化．类似的，也可以在等腰三角形中建立边角之间的联系，我们定义：等腰三角形中底边与腰的比叫做顶角的正对（sad）．如图，在△ABC中，AB=AC，顶角A的正对记作sadA，这时sad A=

．容易知道一个角的大小与这个角的正对值也是相互唯一确定的．
根据上述对角的正对定义，解下列问题：
（1）填空：sad60°=

；
（2）对于0°＜A＜180°，∠A的正对值sadA的取值范围是

；
（3）如图，已知sinA=

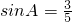，其中A为锐角，试求sadA的值；
（4）设sinA=k，请直接用k的代数式表示sadA的值为

下列各作图题中，可直接用“边边边”条件作出三角形的是（　　）

A．已知腰和底边，求作等腰三角形

B．已知两条直角边，求作等腰三角形

C．已知高，求作等边三角形

D．已知腰长，求作等腰直角三角形

学习过三角函数，我们知道在直角三角形中，一个锐角的大小与两条边长的比值相互唯一确定，因此边长与角的大小之间可以相互转化．类似的，也可以在等腰三角形中建立边角之间的联系，我们定义：等腰三角形中底边与腰的比叫做顶角的正对（sad）．如图，在△ABC中，AB=AC，顶角A的正对记作sadA，这时sad A= $数学公式$ ．容易知道一个角的大小与这个角的正对值也是相互唯一确定的．
根据上述对角的正对定义，解下列问题：
（1）填空：sad60°=，sad90°=，sad120°=；
（2）对于0°＜A＜180°，∠A的正对值sadA的取值范围是；
（3）如图，已知 $数学公式$ ，其中A为锐角，试求sadA的值；
（4）设sinA=k，请直接用k的代数式表示sadA的值为__．

下列各作图题中，可直接用“边边边”条件作出三角形的是（　　）

A．已知腰和底边，求作等腰三角形

B．已知两条直角边，求作等腰三角形

C．已知高，求作等边三角形

D．已知腰长，求作等腰直角三角形

下列各作图题中，可直接用“边边边”条件作出三角形的是

A.已知腰和底边，求作等腰三角形
B.已知两条直角边，求作等腰三角形
C.已知高，求作等边三角形
D.已知腰长，求作等腰直角三角形