Question

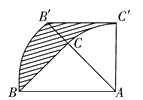
【题目】如图，△ABC是等腰直角三角形，∠ACB=90°，AC=BC=2，把△ABC绕点A按顺时针方向旋转45°后得到△AB′C′，则线段BC在上述旋转过程中所扫过部分（阴影部分）的面积是________.

Answer 1

【答案】

【解析】先根据等腰直角三角形的性质得到∠BAC=45°，AB=AC=2，再根据旋转的性质得∠BAB′=∠CAC′=45°，则点B′、C、A共线，然后根据扇形门口计算，利用线段BC在上述旋转过程中所扫过部分（阴影部分）的面积=S扇形BAB′-S扇形CAC′进行计算即可．

∵△ABC是等腰直角三角形，

∴∠BAC=45°，AB=AC=2，

∵△ABC绕点A按顺时针方向旋转45°后得到△AB′C，

∴∠BAB′=∠CAC′=45°，

∴点B′、C、A共线，

∴线段BC在上述旋转过程中所扫过部分（阴影部分）的面积=S扇形BAB′+S△AB′C-S扇形CAC′-S△ABC

=S扇形BAB′-S扇形CAC′

=

故答案为．