Question

如图，是一个“有理数转换器”（箭头是指数进入转换器的路径，方框是对进入的数进行转换的转换器）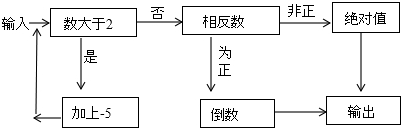

（1）当小明输入3；-4；

5

9

；-201这四个数时，这四次输出的结果分别是？
（2）你认为当输入什么数时，其输出结果是0？
（3）你认为这个“有理数转换器”不可能输出什么数？
（4）有一次，小明在操作的时候，输出的结果是2，你判断一下，小明可能输入的数是什么数？

Answer 1

分析：（1）先判断出3、-4、

5

9

、201与2的大小，再根据所给程序图找出合适的程序进行计算即可；
（2）由此程序可知，当输出0时，因为0的相反数及绝对值均为0，所以应输入0；
（3）由（1）中输出的各数可找出规律；
（4）设输入的数为x，分2＜x＜7、0＜x＜2、当x＜0及x＞7四种情况进行讨论，按输入程序进行解答．

解答：解：（1）∵3＞2，
∴输入3时的程序为：（3-5）=-2＜0，
∴-2的相反数是2＞0，2的倒数是

1

2

，
∴当输入3时，输出

1

2

；
当输入-4时，∵-4＜2，
∴-4的相反数是4＞0，4的倒数是

1

4

，
∴当输入-4时，输出

1

4

；
当输入

5

9

时，

5

9

＜2，
∴其相反数是-

5

9

，其绝对值是

5

9

，
∴当输入

5

9

时，输出

5

9

；
当输入-201时，-201＜2，
∴其相反数是201＞0，其倒数是

1

201

，
∴当输入-201时，输出

1

201

；

（2）∵输出数为0，0的相反数及绝对值均为0，当输入5的倍数时也输出0．
∴应输入0或5n（n为自然数）；

（3）由（1）中输出的各数均为非负数可知，输出的数应为非负数；

（4）∵输出的数为2，
设输入的数为x，
①当2＜x＜7时，（x-5）＜0，其相反数是5-x＞0，其倒数是

1

5-x

=2，解得x=

9

2

；
②当0＜x＜2时，其相反数是-x＜0，其绝对值是x=2，故x=2；
③当x＜0时，其相反数为-x＞0，其倒数是-

1

x

=2，x=-

1

2

．
④当x＞7时，按①的程序可知x=

9

2

+…2n．
总上所述，x的可能值为：

9

2

，2，-

1

2

…x=

9

2

+…2n．

点评：本题考查的是倒数、绝对值及相反数的概念，解答此题的关键是弄清图表中所给的程序，在解（4）时要注意分类讨论．