题目内容
 如图,在正方形网格中画两条直线,那么这两条直线是否垂直?答:________.
如图,在正方形网格中画两条直线,那么这两条直线是否垂直?答:________.
垂直
分析:首先设出小正方形的边长,再利用勾股定理求出AC,BC,AB的长,利用勾股定理逆定理判定△ABC是直角三角形即可得到答案.
解答: 解:设正方形网格每个小正方形的边长为1,连接AB,
解:设正方形网格每个小正方形的边长为1,连接AB,
AC2=32+12=10,
BC2=32+12=10,
AB2=42+22=20,
∵10+10=20,
即:AC2+CB2=AB2,
∴∠ACB=90°,
即:AC⊥CB,
故答案为:垂直.
点评:此题主要考查了勾股定理与勾股定理逆定理,关键是判定AC2+CB2=AB2.
分析:首先设出小正方形的边长,再利用勾股定理求出AC,BC,AB的长,利用勾股定理逆定理判定△ABC是直角三角形即可得到答案.
解答:
 解:设正方形网格每个小正方形的边长为1,连接AB,
解:设正方形网格每个小正方形的边长为1,连接AB,AC2=32+12=10,
BC2=32+12=10,
AB2=42+22=20,
∵10+10=20,
即:AC2+CB2=AB2,
∴∠ACB=90°,
即:AC⊥CB,
故答案为:垂直.
点评:此题主要考查了勾股定理与勾股定理逆定理,关键是判定AC2+CB2=AB2.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
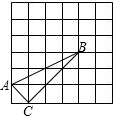 如图,在正方形网格中有△ABC,则sin∠ABC的值等于( )
如图,在正方形网格中有△ABC,则sin∠ABC的值等于( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
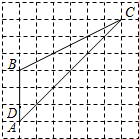 如图,在正方形网格中,点A、B、C、D都是格点,点E是线段AC上任意一点.如果AD=1,那么当AE=
如图,在正方形网格中,点A、B、C、D都是格点,点E是线段AC上任意一点.如果AD=1,那么当AE= 6、如图,在5×5正方形网格中,一条圆弧经过A,B,C三点,那么这条圆弧所在圆的圆心是( )
6、如图,在5×5正方形网格中,一条圆弧经过A,B,C三点,那么这条圆弧所在圆的圆心是( )
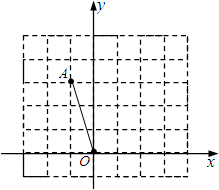 如图,在正方形网格中建立平面直角坐标系,格点O为原点,格点A的坐标为(-1,3).
如图,在正方形网格中建立平面直角坐标系,格点O为原点,格点A的坐标为(-1,3).