题目内容
若实数a,b,c满足条件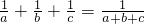 ,则a,b,c中
,则a,b,c中
- A.必有两个数相等
- B.必有两个数互为相反的数
- C.必有两个数互为倒数
- D.每两个数都不等
B
分析:首先把等式去分母得到b2c+bc2+a2c+ac2+a2b+ab2+2abc=0,用分组分解法将上式左边分解因式(a+b)(b+c)(a+c)=0,
得到a+b=0,b+c=0,a+c=0,根据相反数的定义即可选出选项.
解答: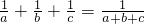 ,
,
去分母并整理得:b2c+bc2+a2c+ac2+a2b+ab2+2abc=0,
即:(b2c+2abc+a2c)+(bc2+ac2)+(a2b+ab2)=0,
∴c(a+b)2+c2(a+b)+ab(a+b)=0,
(a+b)(ac+bc+c2+ab)=0,
(a+b)(b+c)(a+c)=0,
即:a+b=0,b+c=0,a+c=0,
必有两个数互为相反数,
故选B.
点评:本题主要考查了分式的基本性质,因式分解的分组分解法,相反数,单项式乘多项式,多项式乘多项式,完全平方公式等知识点,去分母后分解因式是解此题的关键.
分析:首先把等式去分母得到b2c+bc2+a2c+ac2+a2b+ab2+2abc=0,用分组分解法将上式左边分解因式(a+b)(b+c)(a+c)=0,
得到a+b=0,b+c=0,a+c=0,根据相反数的定义即可选出选项.
解答:
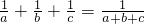 ,
,去分母并整理得:b2c+bc2+a2c+ac2+a2b+ab2+2abc=0,
即:(b2c+2abc+a2c)+(bc2+ac2)+(a2b+ab2)=0,
∴c(a+b)2+c2(a+b)+ab(a+b)=0,
(a+b)(ac+bc+c2+ab)=0,
(a+b)(b+c)(a+c)=0,
即:a+b=0,b+c=0,a+c=0,
必有两个数互为相反数,
故选B.
点评:本题主要考查了分式的基本性质,因式分解的分组分解法,相反数,单项式乘多项式,多项式乘多项式,完全平方公式等知识点,去分母后分解因式是解此题的关键.

练习册系列答案
相关题目