Question

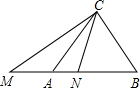已知Rt△ABC中，∠ACB=90°，CA=CB，M在BA延长线上，N在AB上，且∠MCN=45°，AM=2，BN=3，则MN=________．

Answer 1

分析：根据△ABC为等腰直角三角形的特点，解：过C点作CD⊥BM，设AN=x，则AB=AN+BN=3+x，在△CDN中，由勾股定理表CN²=CD²+ND²，由△NAC∽△NCM，利用相似比得CN²=MN•AN，两式结合求x即可．
解答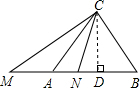：解：过C点作CD⊥BM，垂足为D，
设AN=x，则AB=AN+BN=3+x，
又∵∠ACB=90°，CA=CB，
∴AD=BD=CD=AB=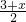，ND=AD-AN=，
由勾股定理，得CN²=CD²+ND²，①
∵∠NAC=MCN=45°，∠ANC=∠CNM，
∴△NAC∽△NCM，
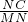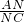∴=，即CN²=MN•AN=（2+x）x，②
由①②得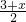：（）²+（）²=（2+x）x，
解得x=-2，
MN=AM+AN=2+x=．
故答案为：．
点评：本题考查了特殊三角形的性质，相似三角形的判定与性质，勾股定理的运用．关键是通过设AN=x，由已知条件表示其它的线段，利用勾股定理及相似求解．