Question

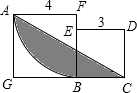如图，扇形AFB恰为一个圆的

1

4

，BCDE是正方形，AFBG也是正方形，则图中阴影部分的面积是

 

（π以3.14计算）．

Answer 1

分析：先设靠近点G的空白部分面积为x，再根据S_阴影=S_△ACG-x=

1

2

CG•AG-（S_{正方形AFBG}-S_扇形ABF）进行解答即可．

解答：解：如图所示，设靠近点G的空白部分面即为x，
∵正方形AFBG与正方形BCDE的边长分别是4，3，
∴CG=GB+BC=4+3=7，
∴S_阴影=S_△ACG-x
=

1

2

CG•AG-（S_{正方形AFBG}-S_扇形ABF）
=

1

2

×7×4-（4×4-

1

4

π×4²）
=14-（16-4π）
≈-2+4×3.14
=10.56．
故答案为10.56．

点评：本题考查的是面积及等积变换，解答此题的关键是把阴影部分的面积转化为三角形、正方形及扇形的面积之间的和差关系．