题目内容
如图,⊙O是△ABC的外接圆,AB是⊙O的直径,D为⊙O上的一点,OD⊥AC,垂足为E,连接BD.
(1)求证:BD平分∠ABC;
(2)当∠ODB=30°时,求证:BC=OD.

证明:(1)∵OD⊥AC,OD为半径,
∴ ∴∠CBD=∠ABD,(4分)
∴∠CBD=∠ABD,(4分)
∴BD平分∠ABC.(5分)
(2)∵OB=OD,∴∠OBD=∠ODB=30°,
∴∠AOD=∠OBD+∠ODB=30°+30°=60°.(7分)
又∵OD⊥AC于E,∴∠OEA=90°,
∴∠A=180°-∠OEA-∠AOD=180°-90°-60°=30°.(9分)
又∵AB为⊙O的直径,∴∠ACB=90°,
则在Rt△ACB中,BC= AB,∵OD=
AB,∵OD= AB,∴BC=OD.(12分)
AB,∴BC=OD.(12分)

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
 与
与 互为相反数,则
互为相反数,则 的值为( )
的值为( ) B.-
B.- B.
B.
 C.
C. D.1
D.1 
 ,正方形OA
,正方形OA BC与正方形ODEF是位似图形,O为位似中心相似比为1∶
BC与正方形ODEF是位似图形,O为位似中心相似比为1∶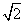 ,点A的坐标为(1,0),则E点的坐标为( )
,点A的坐标为(1,0),则E点的坐标为( )
 ,
,
 O的直径,若∠P=46°,则∠BAC=______.
O的直径,若∠P=46°,则∠BAC=______.
 D.-
D.-

 四组点中,可以在同一个正比例函数图象上的一组点是( )
四组点中,可以在同一个正比例函数图象上的一组点是( )