题目内容
已知：如图，把长方形纸片ABCD沿EF折叠，使D、C分别落在D′、C′的位置，若∠EFB=65°，则∠AED′的度数为
- A.20°
- B.30°
- C.40°
- D.50°
D
分析：根据平行线的性质可得∠EFB=∠DEF=65°，再根据折叠可得∠D′EF=∠DEF=65°，则∠AED′=180°-∠DEF-∠FED′．
解答：∵四边形ABCD是矩形，
∴AD∥BC，
∴∠EFB=∠DEF=65°，
根据折叠可得∠D′EF=∠DEF=65°，
∴∠AED′=180°-65°×2=50°，
故选：D．
点评：此题主要考查了平行线的性质，关键是掌握两直线平行，内错角相等．
分析：根据平行线的性质可得∠EFB=∠DEF=65°，再根据折叠可得∠D′EF=∠DEF=65°，则∠AED′=180°-∠DEF-∠FED′．
解答：∵四边形ABCD是矩形，
∴AD∥BC，
∴∠EFB=∠DEF=65°，
根据折叠可得∠D′EF=∠DEF=65°，
∴∠AED′=180°-65°×2=50°，
故选：D．
点评：此题主要考查了平行线的性质，关键是掌握两直线平行，内错角相等．
练习册系列答案
阅读快车系列答案
相关题目
已知：如图，把长方形纸片ABCD沿EF折叠后．点D与点B重合，点C落在点C′的位置上．若∠1=60°，BE=2．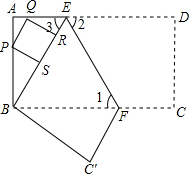
已知：如图，把长方形纸片ABCD沿EF折叠后，点D与点B重合，点C落在点C′的位置上．若∠1=60°，AE=1．
已知：如图，把长方形纸片ABCD沿EF折叠，使D、C分别落在D′、C′的位置，若∠EFB=65°，则∠AED′的度数为（ ）
已知：如图，把长方形纸片ABCD沿EF折叠后．点D与点B重合，点C落在点C′的位置上．若∠1=60°，BE=2．