题目内容
 如图,一段河坝的断面为梯形ABCD,根据图中数据推测,河底宽AD=
如图,一段河坝的断面为梯形ABCD,根据图中数据推测,河底宽AD=分析:在Rt△CED中,已知了铅直高度以及坡度比,可求出DE的长;过B作BF⊥AD于F,在Rt△ABF中,根据铅直高度和坡角的度数,可求出AF的长.AD=AF+BC+DE.
解答: 解:过B作BF⊥AD于F.
解:过B作BF⊥AD于F.
Rt△CED中,CE=4,i=
=
,
∴DE=
CE=4
.
Rt△ABF中,BF=4,∠A=45°,
∴AF=BF=4.
故AD=AF+EF+DE=4+4+4
=8+4
(米).
 解:过B作BF⊥AD于F.
解:过B作BF⊥AD于F.Rt△CED中,CE=4,i=
| CE |
| DE |
| 1 | ||
|
∴DE=
| 3 |
| 3 |
Rt△ABF中,BF=4,∠A=45°,
∴AF=BF=4.
故AD=AF+EF+DE=4+4+4
| 3 |
| 3 |
点评:作“两高”构造出直角三角形和矩形,是解有关梯形问题时常作的辅助线.

练习册系列答案
相关题目
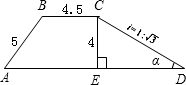 如图,一段河坝的断面为梯形ABCD,试根据图中数据,求出坡角α和坝底宽AD.(单位米,结果精确到0.1米)
如图,一段河坝的断面为梯形ABCD,试根据图中数据,求出坡角α和坝底宽AD.(单位米,结果精确到0.1米) 如图,一段河坝的断面为梯形ABCD,迎水坡面BC的坡度为
如图,一段河坝的断面为梯形ABCD,迎水坡面BC的坡度为 如图,一段河坝的断面为梯形ABCD,试根据图中数据,求出坡角α和坝底宽AD.(单位米,结果精确到0.1米)
如图,一段河坝的断面为梯形ABCD,试根据图中数据,求出坡角α和坝底宽AD.(单位米,结果精确到0.1米)