题目内容
 如图Rt△ABC中,∠ACB=90°,点D在AB上,且AD=AC,若∠A=40°,则∠ACD=________,∠DCB=________,若∠A=α,则∠BCD=________,由此我们可得出∠BCD与∠A的关系是∠BCD=________∠A.
如图Rt△ABC中,∠ACB=90°,点D在AB上,且AD=AC,若∠A=40°,则∠ACD=________,∠DCB=________,若∠A=α,则∠BCD=________,由此我们可得出∠BCD与∠A的关系是∠BCD=________∠A.
70° 20° 

分析:依题意,已知AD=AC,∠A=40°,易求出∠ACD,∠DCB的度数.又根据∠A=α,利用三角形内角和定理可求出∠BCD的值.
解答:∵AD=AC,∠A=40°,则∠ACD=(180°-40°)× =70°,
=70°,
∵∠ACB=90°,∴∠DCB=20°,
若∠A=α,则∠BCD=90°- =
= ,根据此过程即可发现∠BCD=
,根据此过程即可发现∠BCD= ∠A.
∠A.
故答案为70°,20°, ,
, .
.
点评:此题主要是运用了三角形的内角和定理以及余角的定义.


分析:依题意,已知AD=AC,∠A=40°,易求出∠ACD,∠DCB的度数.又根据∠A=α,利用三角形内角和定理可求出∠BCD的值.
解答:∵AD=AC,∠A=40°,则∠ACD=(180°-40°)×
 =70°,
=70°,∵∠ACB=90°,∴∠DCB=20°,
若∠A=α,则∠BCD=90°-
 =
= ,根据此过程即可发现∠BCD=
,根据此过程即可发现∠BCD= ∠A.
∠A.故答案为70°,20°,
 ,
, .
.点评:此题主要是运用了三角形的内角和定理以及余角的定义.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
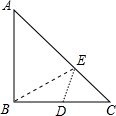 如图Rt△ABC中,AB=BC=4,D为BC的中点,在AC边上存在一点E,连接ED,EB,则△BDE周长的最小值为( )
如图Rt△ABC中,AB=BC=4,D为BC的中点,在AC边上存在一点E,连接ED,EB,则△BDE周长的最小值为( )A、2
| ||
B、2
| ||
C、2
| ||
D、2
|
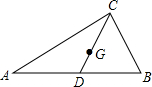 如图Rt△ABC中,∠C=90°,AC=8,BC=6,CD为AB边上的中线,点G是重心,则DG=
如图Rt△ABC中,∠C=90°,AC=8,BC=6,CD为AB边上的中线,点G是重心,则DG= 如图Rt△ABC中,∠C=90°,AC=12cm,BC=6cm,点P从B出发,以1cm/s的速度向C运动,同时点Q从C出发,以1cm/s的速度向A运动,问几秒时PQ的长为2
如图Rt△ABC中,∠C=90°,AC=12cm,BC=6cm,点P从B出发,以1cm/s的速度向C运动,同时点Q从C出发,以1cm/s的速度向A运动,问几秒时PQ的长为2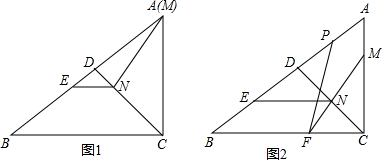
 已知:如图Rt△ABC中,∠C=Rt∠,AB=5,BC=4.
已知:如图Rt△ABC中,∠C=Rt∠,AB=5,BC=4.