题目内容
【题目】如图,把平面内一条数轴![]() 绕原点
绕原点![]() 逆时针旋转角
逆时针旋转角![]() 得到另一条数轴
得到另一条数轴![]() 轴和
轴和![]() 轴构成一个平面斜坐标系.过点
轴构成一个平面斜坐标系.过点![]() 作
作![]() 轴的平行线,交
轴的平行线,交![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 轴的平行线,交
轴的平行线,交![]() 轴于点
轴于点![]() .若点
.若点![]() 在
在![]() 轴上对应的实数为
轴上对应的实数为![]() ,点
,点![]() 在
在![]() 轴上对应的实数为
轴上对应的实数为![]() ,则成有序实数对
,则成有序实数对![]() 为点
为点![]() 的斜坐标.
的斜坐标.
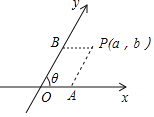
(1)在某平面斜坐标系中,已知![]() ,点
,点![]() 的斜坐标为
的斜坐标为![]() ,点
,点![]() 与点
与点![]() 关于
关于![]() 轴对称,求点
轴对称,求点![]() 的斜坐标.
的斜坐标.
(2)某平面斜坐标系中,已知点![]() ,求出点
,求出点![]() 关于
关于![]() 轴、
轴、![]() 轴的对称点
轴的对称点![]() 点、
点、![]() 点的斜坐标.(用含
点的斜坐标.(用含![]() 及
及![]() 的式子表示).
的式子表示).
(3)直接写出点![]() 关于原点对称的点的斜坐标是_________.
关于原点对称的点的斜坐标是_________.
【答案】(1) (5,-3); (2)![]() ,
,![]() ; (3)
; (3)![]()
【解析】
(1)如图,作点P关于x轴的对称点N,连接PN交x轴于F,作NC∥x轴交y轴于C,作ND∥y轴交x轴于D.求出OC,OD即可解决问题;
(2)利用(1)中的方法解决问题即可;
(3)根据斜坐标的定义写出坐标即可.
(1)如图,作点P关于x轴的对称点N,连接PN交x轴于F,作NC∥x轴交y轴于C,作ND∥y轴交x轴于D.
∵DN∥BC∥PA,
∴∠PAF=∠NDF,
∵PF=NF,∠AFP=∠NFD,
∴△AFP≌△DFN(AAS),
∴AF=DF,PA=DN=OC=b,
∵在Rt△AFP中,∠PAF=∠BOA=θ=60°,
∴AF=DF=bcos60°=![]() b,
b,
∴OD=OA+ AF+DF =![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴点N的斜坐标为(5,-3);
(2)如图,作点P关于x轴的对称点Q,连接PQ交x轴于F,作QC∥x轴交y轴于C,作QD∥y轴交x轴于D.

∵DQ∥BC∥PA,
∴∠PAF=∠QDF,
∵PF=QF,∠AFP=∠QFD,
∴△AFP≌△DFQ(AAS),
∴AF=DF,PA=DQ=OC=y,
∵在Rt△AFP中,∠PAF=∠BOA=θ,
∴AF=DF=![]() ,
,
∴DO=OA+AF+FD=![]()
∴点Q的斜坐标为![]() ,
,
如图,作点P关于y轴的对称点R,连接PR交![]() 轴于E,作RH∥
轴于E,作RH∥![]() 轴交y轴于H,作RG∥
轴交y轴于H,作RG∥![]() 轴交
轴交![]() 轴于G.
轴于G.

同理可证得△EBP≌△EHR(AAS),
∴BE=EH,PB=RH=OA=![]() ,
,
∵在Rt△EBP中,∠EBP=∠BOA=θ,
∴BE=EH =![]() cos
cos![]() ,
,
∴HO=OB+BE+EH=![]() ,
,
∴点R的坐标为![]() ;
;
(3)如图,点P关于原点的对称点![]() ,作
,作![]() ∥
∥![]() 轴交
轴交![]() 轴于M.
轴于M.

∵![]() ∥PB∥OA,
∥PB∥OA,![]()
∴△![]() ≌△PBO,
≌△PBO,
∴![]() ,
,![]() ,
,
∴![]() 关于原点对称的点的斜坐标是
关于原点对称的点的斜坐标是![]() ,
,
故答案为:![]() .
.







