��Ŀ����
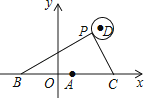
����Ŀ����ͼ�����κ���y=x2��4x��ͼ����x�ᡢֱ��y=x��һ������ֱ�Ϊ��A��B��CD���߶�OB�ϵ�һ���߶Σ���CD=2������C��D����ֱ�߶�ƽ����y�ᣬ���������ཻ�ڵ�F��E������EF�� 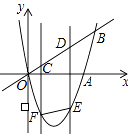
��1����A������Ϊ �� �߶�OB�ij�=��
��2�����C�ĺ�����Ϊm �ٵ��ı���CDEF��ƽ���ı���ʱ����m��ֵ��
������AC��AD����mΪ��ֵʱ����ACD���ܳ���С������������Сֵ��
���𰸡�
��1����4��0����5 ![]()
��2���⣺�١ߵ�C�ĺ�����Ϊm����CF��DE��y�ᣬ
��C��m��m����F��m��m2��4m����
�֡�CD=2����CD���߶�OB�ϵ�һ���߶Σ�
��D��m+ ![]() ��m+
��m+ ![]() ����E��m+
����E��m+ ![]() ����m+
����m+ ![]() ��2��4��m+
��2��4��m+ ![]() ������
������
��CF=m����m+ ![]() ����DE=m+
����DE=m+ ![]() ��[��m+
��[��m+ ![]() ��2��4��m+
��2��4��m+ ![]() ��]��
��]��
�ߵ��ı���CDEF��ƽ���ı���ʱ��CF=DE��
��m����m+ ![]() ��=m+
��=m+ ![]() ��[��m+
��[��m+ ![]() ��2��4��m+
��2��4��m+ ![]() ��]��
��]��
���m= ![]() ��
��
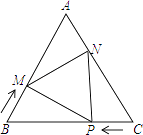
����ͼ��ʾ������A��CD��ƽ���ߣ�����D��AC��ƽ���ߣ����ڵ�G�����ı���ACDG��ƽ���ı��Σ�
��AC=DG��
����A����ֱ��OB�ĶԳƵ�A'������A'D����A'D=AD��
�൱A'��D��G���㹲��ʱ��A'D+DG=A'G��̣���ʱAC+AD��̣�
��A��4��0����AG=CD=2��
��A'��0��4����G��4+ ![]() ��
�� ![]() ����
����
��ֱ��A'G�Ľ���ʽΪy=kx+b����
![]() �����
����� 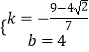 ��
��
��ֱ��A'G�Ľ���ʽΪy=�� ![]() x+4��
x+4��
�ⷽ���� 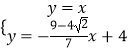 ���ɵ�
���ɵ�  ��
��
��D��2+ ![]()
![]() ��2+
��2+ ![]()
![]() ����
����
��CD=2����CD���߶�OB�ϵ�һ���߶Σ�
��C��2�� ![]() ��2��
��2�� ![]() ����
����
���C�����m=2�� ![]() ��
��
��A��4��0����C��2�� ![]() ��2��
��2�� ![]() ���ɵã�AC=
���ɵã�AC= ![]() =3��
=3��
��A��4��0����D��2+ ![]()
![]() ��2+
��2+ ![]()
![]() ���ɵã�AD=
���ɵã�AD= ![]() =3��
=3��
�֡�CD=2��
���ACD���ܳ�=CD+AC+AD=2+3+3=8��
�ʵ�m=2�� ![]() ʱ����ACD���ܳ���С�������СֵΪ8��
ʱ����ACD���ܳ���С�������СֵΪ8��
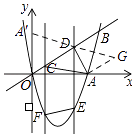

���������⣺��1����y=x2��4x�У���y=0����0=x2��4x�� ���x1=0��x2=4��
��A��4��0����
�ⷽ���� ![]() ���ɵ�
���ɵ�![]() ��
�� ![]() ��
��
��B��5��5����
��OB= ![]() =5
=5 ![]() ��
��
���Դ��ǣ���4��0����5 ![]() ��
��
��1������y=x2��4x�У���y=0����0=x2��4x�������A��4��0�����ⷽ���� ![]() ���ɵ�B��5��5���������ó�OB�ij�����2���ٸ���C��m��m����F��m��m2��4m�����ɵ�CF=m����m+
���ɵ�B��5��5���������ó�OB�ij�����2���ٸ���C��m��m����F��m��m2��4m�����ɵ�CF=m����m+ ![]() ��������D��m+
��������D��m+ ![]() ��m+
��m+ ![]() ����E��m+
����E��m+ ![]() ����m+
����m+ ![]() ��2��4��m+
��2��4��m+ ![]() �������ɵ�DE=m+
�������ɵ�DE=m+ ![]() ��[��m+
��[��m+ ![]() ��2��4��m+
��2��4��m+ ![]() ��]�������ݵ��ı���CDEF��ƽ���ı���ʱ��CF=DE�����m��ֵ���ɣ����ȹ���A��CD��ƽ���ߣ�����D��AC��ƽ���ߣ����ڵ�G�����ı���ACDG��ƽ���ı��Σ��ó�AC=DG��������A����ֱ��OB�ĶԳƵ�A'������A'D����A'D=AD�����ݵ�A'��D��G���㹲��ʱ��A'D+DG=A'G��̣��ɵô�ʱAC+AD��̣�Ȼ�����ֱ��A'G�Ľ���ʽΪy=��
��]�������ݵ��ı���CDEF��ƽ���ı���ʱ��CF=DE�����m��ֵ���ɣ����ȹ���A��CD��ƽ���ߣ�����D��AC��ƽ���ߣ����ڵ�G�����ı���ACDG��ƽ���ı��Σ��ó�AC=DG��������A����ֱ��OB�ĶԳƵ�A'������A'D����A'D=AD�����ݵ�A'��D��G���㹲��ʱ��A'D+DG=A'G��̣��ɵô�ʱAC+AD��̣�Ȼ�����ֱ��A'G�Ľ���ʽΪy=�� ![]() x+4���ⷽ����ɵ�D��2+
x+4���ⷽ����ɵ�D��2+ ![]()
![]() ��2+
��2+ ![]()
![]() ����C��2��
����C��2�� ![]() ��2��
��2�� ![]() �����������������빫ʽ����á�ACD���ܳ�����Сֵ��
�����������������빫ʽ����á�ACD���ܳ�����Сֵ��
�����㾫����������Ҫ��������������������Ľ����ƽ���ı��ε��ж������ʵ����֪ʶ�㣬��Ҫ����һԪ���η��̵Ľ������Ӧ�Ķ��κ�����ͼ����x��Ľ������꣮���һԪ���η����е�b2-4ac���ڶ��κ����б�ʾͼ����x���Ƿ��н��㣮��b2-4ac>0ʱ��ͼ����x�����������㣻��b2-4ac=0ʱ��ͼ����x����һ�����㣻��b2-4ac<0ʱ��ͼ����x��û�н��㣮����һֱ�߹�ƽ���ı������Խ��ߵĽ��㣬������ֱ�߱�һ��Ա߽��µ��߶��ԶԽ��ߵĽ���Ϊ�е㣬����������ֱ�߶��ȷִ�ƽ���ı��ε����������ȷ�����⣮

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�