ЬтФПФкШн
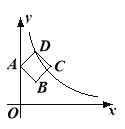
ЁОЬтФПЁПШчЭМЃЌRt![]() ABCжаЃЌЁЯCЃН90ЁуЃЌACЃН10ЃЌBCЃН16ЃЎЖЏЕуPвдУПУы3ИіЕЅЮЛЕФЫйЖШДгЕуAПЊЪМЯђЕуCвЦЖЏЃЌжБЯпlДггыACжиКЯЕФЮЛжУПЊЪМЃЌвдЯрЭЌЕФЫйЖШбиCBЗНЯђЦНаавЦЖЏЃЌЧвЗжБ№гыCBЃЌABБпНЛгкEЃЌFСНЕуЃЌЕуPгыжБЯпlЭЌЪБГіЗЂЃЌЩшдЫЖЏЕФЪБМфЮЊtУыЃЌЕБЕуPвЦЖЏЕНгыЕуCжиКЯЪБЃЌЕуPКЭжБЯпlЭЌЪБЭЃжЙдЫЖЏЃЎдквЦЖЏЙ§ГЬжаЃЌНЋ
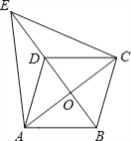
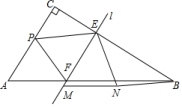
ABCжаЃЌЁЯCЃН90ЁуЃЌACЃН10ЃЌBCЃН16ЃЎЖЏЕуPвдУПУы3ИіЕЅЮЛЕФЫйЖШДгЕуAПЊЪМЯђЕуCвЦЖЏЃЌжБЯпlДггыACжиКЯЕФЮЛжУПЊЪМЃЌвдЯрЭЌЕФЫйЖШбиCBЗНЯђЦНаавЦЖЏЃЌЧвЗжБ№гыCBЃЌABБпНЛгкEЃЌFСНЕуЃЌЕуPгыжБЯпlЭЌЪБГіЗЂЃЌЩшдЫЖЏЕФЪБМфЮЊtУыЃЌЕБЕуPвЦЖЏЕНгыЕуCжиКЯЪБЃЌЕуPКЭжБЯпlЭЌЪБЭЃжЙдЫЖЏЃЎдквЦЖЏЙ§ГЬжаЃЌНЋ![]() PEFШЦЕуEФцЪБеыа§зЊЃЌЪЙЕУЕуPЕФЖдгІЕуMТфдкжБЯпlЩЯЃЌЕуFЕФЖдгІЕуМЧЮЊЕуNЃЌСЌНгBNЃЌЕБBNЁЮPEЪБЃЌtЕФжЕЮЊ_____ЃЎ
PEFШЦЕуEФцЪБеыа§зЊЃЌЪЙЕУЕуPЕФЖдгІЕуMТфдкжБЯпlЩЯЃЌЕуFЕФЖдгІЕуМЧЮЊЕуNЃЌСЌНгBNЃЌЕБBNЁЮPEЪБЃЌtЕФжЕЮЊ_____ЃЎ
ЁОД№АИЁП![]()
ЁОНтЮіЁП
зїNHЁЭBCгкHЃЎЪзЯШжЄУїЁЯPECЃНЁЯNEBЃНЁЯNBEЃЌЭЦГіEHЃНBHЃЌИљОнcosЁЯPECЃНcosЁЯNEBЃЌЭЦГі![]() ЃН
ЃН![]() ЃЌгЩДЫЙЙНЈЗНГЬНтОіЮЪЬтМДПЩЃЎ
ЃЌгЩДЫЙЙНЈЗНГЬНтОіЮЪЬтМДПЩЃЎ
НтЃКзїNHЁЭBCгкHЃЎ
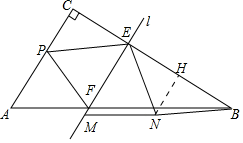
ЁпEFЁЭBCЃЌЁЯPEFЃНЁЯNEFЃЌ
ЁрЁЯFECЃНЁЯFEBЃН90ЁуЃЌ
ЁпЁЯPEC+ЁЯPEFЃН90ЁуЃЌЁЯNEB+ЁЯFENЃН90ЁуЃЌ
ЁрЁЯPECЃНЁЯNEBЃЌ
ЁпPEЁЮBNЃЌ
ЁрЁЯPECЃНЁЯNBEЃЌ
ЁрЁЯNEBЃНЁЯNBEЃЌ
ЁрNEЃНNBЃЌ
ЁпHNЁЭBEЃЌ
ЁрEHЃНBHЃЌ
ЁрcosЁЯPECЃНcosЁЯNEBЃЌ
Ёр![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁпEFЁЮACЃЌ
Ёр![]() ЃН
ЃН![]() ЃЌ
ЃЌ
Ёр![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁрEFЃНENЃН![]() (16Љ3t)ЃЌ
(16Љ3t)ЃЌ
Ёр![]() ЃН
ЃН ЃЌ
ЃЌ
ећРэЕУЃК63t2Љ960t+1600ЃН0ЃЌ
НтЕУtЃН![]() Лђ
Лђ![]() (ЩсЦњ)ЃЌ
(ЩсЦњ)ЃЌ
ЙЪД№АИЮЊЃК![]() ЃЎ
ЃЎ

 99Мг1СьЯШЦкФЉЬибЕОэЯЕСаД№АИ
99Мг1СьЯШЦкФЉЬибЕОэЯЕСаД№АИ АйЧПУћаЃЦкФЉГхДЬ100ЗжЯЕСаД№АИ
АйЧПУћаЃЦкФЉГхДЬ100ЗжЯЕСаД№АИ КУГЩМЈ1Мг1ЦкФЉГхДЬ100ЗжЯЕСаД№АИ
КУГЩМЈ1Мг1ЦкФЉГхДЬ100ЗжЯЕСаД№АИ Н№зДдЊМЈгХКУОэЯЕСаД№АИ
Н№зДдЊМЈгХКУОэЯЕСаД№АИЁОЬтФПЁПФГбЇаЃзщжЏНЁПЕжЊЪЖОКШќЃЌУПАрВЮМгОКШќЕФШЫЪ§ЯрЭЌЃЌГЩМЈЮЊ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЫФИіЕШМЖЃЌЦфжаЯргІЕШМЖЕФЕУЗжвРДЮМЧЮЊ100ЗжЃЌ90ЗжЃЌ80ЗжЃЌ70ЗжЃЌЦфжа100ЗжКЭ90ЗжЮЊгХау.бЇаЃНЋАЫФъМЖвЛАрКЭЖўАрЕФГЩМЈећРэВЂЛцжЦГЩШчЯТЕФЭГМЦЭМгыЭГМЦБэ.
ЫФИіЕШМЖЃЌЦфжаЯргІЕШМЖЕФЕУЗжвРДЮМЧЮЊ100ЗжЃЌ90ЗжЃЌ80ЗжЃЌ70ЗжЃЌЦфжа100ЗжКЭ90ЗжЮЊгХау.бЇаЃНЋАЫФъМЖвЛАрКЭЖўАрЕФГЩМЈећРэВЂЛцжЦГЩШчЯТЕФЭГМЦЭМгыЭГМЦБэ.
вЛАрОКШќГЩМЈЭГМЦЭМ
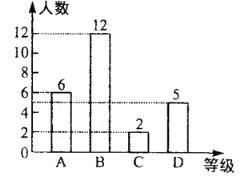
ЖўАрОКШќГЩМЈЭГМЦЭМ
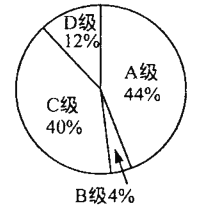
вЛАрКЭЖўАрОКШќГЩМЈЭГМЦБэЃЈВПЗжПеШБЃЉ
ГЩМЈ АрМЖ | жкЪ§ | жаЮЛЪ§ | гХауТЪ | ЦНОљЗж |
вЛАр | 90 |
|
| 87.6 |
ЖўАр |
| 80 |
|
|
ЧыИљОнвдЩЯЭМБэЕФаХЯЂНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉЧѓ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЕФжЕ.
ЕФжЕ.
ЃЈ2ЃЉШєШЋаЃЙВга750УћбЇЩњВЮМгОКШќЃЌЙРМЦГЩМЈгХауЕФбЇЩњгаЖрЩйШЫЃП