题目内容
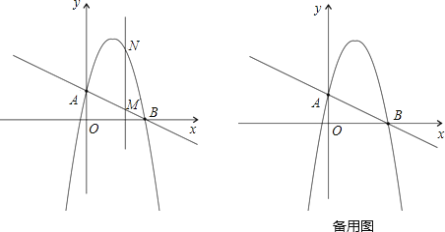
【题目】如图,一次函数y=-![]() x+2分别交y轴、x轴于A、B两点,抛物线y=-
x+2分别交y轴、x轴于A、B两点,抛物线y=-![]() +bx+c过A、B两点.
+bx+c过A、B两点.
(1)求这个抛物线的解析式;
(2)作垂直x轴的直线x=t,在第一象限交直线AB于M,交这个抛物线于N.求当t取何值时,MN有最大值?最大值是多少?
(3)在(2)的情况下,以A、M、N、D为顶点作平行四边形,求第四个顶点D的坐标.
【答案】(1)、y=-![]() +3.5x+2;(2)、t=2时,最大值为4;(3)、(0,6),(0,-2)或(4,4)
+3.5x+2;(2)、t=2时,最大值为4;(3)、(0,6),(0,-2)或(4,4)
【解析】
试题分析:(1)、根据题意得出点A和点B的坐标,然后将两点代入函数解析式得出b和c的值,得出函数解析式;(2)、设出点M和点N的坐标,从而得出MN的长度,根据二次函数的性质得出最大值;(3)、根据题意得出点A、点M和点N的坐标,然后根据平行四边形的性质得出三种情况,从而求出点D的坐标.
试题解析:(1)、求A、B点的坐标为:A(0,2),B(4,0) 将x=0,y=2代入y=-![]() +bx+c得c=2
+bx+c得c=2
将x=4,y=0代入y=-![]() +bx+c得0=-16+4b+2,解得b=3.5
+bx+c得0=-16+4b+2,解得b=3.5
∴抛物线解析式为:y=-![]() +3.5x+2
+3.5x+2
(2)、由题意,易得M(t,-![]() t+2), N(t, -
t+2), N(t, -![]() +3.5t+2),从而MN=-
+3.5t+2),从而MN=-![]() +3.5t+2-(-
+3.5t+2-(-![]() t+2)=-
t+2)=-![]() +4t=-
+4t=-![]()
∴当t=2时,MN有最大值4
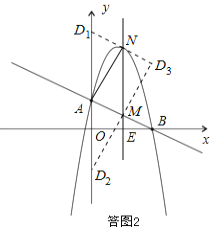
(3) 、由(2)可知,A(0,2),M(2,1),N(2,5).
以A、M、N、D为顶点作平行四边形,D点的可能位置有三种情形,如答图2所示.
当D在y轴上时,设D的坐标为(0,a) 由AD=MN,得|a-2|=4,解得![]() =6,
=6,![]() =-2,
=-2,
从而D为(0,6)或D(0,-2)
当D不在y轴上时,由图可知D3为D1N与D2M的交点,求出直线D1N与D2M的解析式
由两解析式联立解得D为(4,4) 故所求的D点坐标为(0,6),(0,-2)或(4,4)

 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案