题目内容
在△ABC中,已知∠BAC=45°,高线CD与高线AE相交于点H,连接DE.(1)如图1,△ABC为锐角三角形时,求证:AE-CE=
 DE;
DE;(2)如图2,在(1)的条件下,作∠AEC的平分线交AC于点F,连接DF交AE于点G,若BD=
 CF,AE=6,求GH的长.
CF,AE=6,求GH的长.
【答案】分析:(1)过点D作DN⊥DE交AE于点N,易证得△ADN≌△CDE,由全等三角形的对应边相等,可得CE=AN,DE=DN,即可得△DEN是等腰直角三角形,则可证得AE-CE=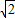 DE;
DE;
(2)易证得△DBE∽△CFE,根据相似三角形的对应边成比例,可得DE=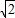 EC,设EC=x,则DE=
EC,设EC=x,则DE=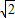 x,由(1)结论可得:6-x=2x,则可求得DE等线段的长度,又由△ADH≌△CDB,可求得DH与CA的长,然后过F做FM∥AE交CD于点M,由相似三角形的对应边成比例,即可求得GH的长.
x,由(1)结论可得:6-x=2x,则可求得DE等线段的长度,又由△ADH≌△CDB,可求得DH与CA的长,然后过F做FM∥AE交CD于点M,由相似三角形的对应边成比例,即可求得GH的长.
解答: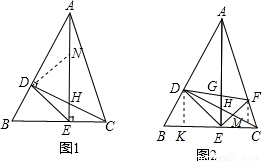 解:(1)过点D作DN⊥DE交AE于点N.
解:(1)过点D作DN⊥DE交AE于点N.
∵CD⊥AD,∠BAC=45°,
∴∠ACD=45°,
∴AD=CD.
∵∠ADN+∠NDC=∠ADC=90°=∠NDC+∠EDC,
∴∠ADN=∠EDC,
∵高线CD与高线AE相交于点H,
∴∠DAH+∠B=90°,∠DCB+∠B=90°,
∴∠DAH=∠DCB,
在△ADN和△CDE中,
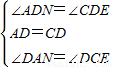 ,
,
∴△ADN≌△CDE(ASA),
∴CE=AN,DE=DN,
∴∠DEN=45°,EN= DE,
DE,
∴AE-EC=AE-AN=EN=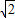 DE;
DE;
(2)由(1)可得:∠BED=45°,
∵AE⊥BC,
∴∠AEC=90°,EF平分∠AEC,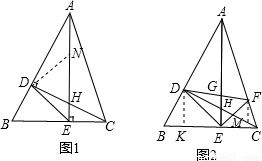
∴∠CEF=45°,
∴∠CEF=∠BED,∠CFE=180°-∠CEF-∠ACB=180°-45°-∠ACB,
∵∠BAC=45°,
∴∠B=180°-∠BAC-∠ACB=180°-45°-∠ACB,
∴∠B=∠CFE,
∴△DBE∽△CFE,
∴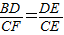 ,
,
∵BD=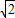 CF,
CF,
∴DE=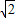 EC,
EC,
设EC=x,则DE=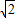 x,
x,
由(1)结论可得:6-x=2x,
解得:x=2,
∴EC=2,DE=2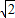 ,
,
过D作DK⊥BC于K,
∵∠DEB=45°,
∴DK=EK=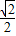 DE=2,
DE=2,
∴CK=EK+EC=4,
∴tan∠DCK=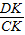 =
= =
= ,CD=
,CD=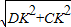 =2
=2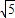 ,
,
∴BD= CD=
CD=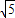 ,BC=5,
,BC=5,
∴CF=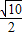 ,
,
∵AE∥DK,EK=EC,
∴EH= DK=1,CH=
DK=1,CH= CD=
CD=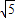 ,
,
∴AH=AE-EH=5,
∴AH=BC,
由(1)得:∠DAH=∠DCB,AD=BC,
在△ADH和△CDB中,
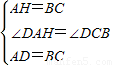 ,
,
∴△ADH≌△CDB(SAS),
∴DH=BD=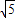 ,CA=
,CA=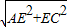 =2
=2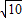 ,
,
过F做FM∥AE交CD于点M,
则△CFM∽△CAH,
∴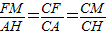 =
= ,
,
∴FM= ,CM=
,CM=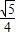 ,MH=
,MH=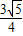 ,
,
又∵GH∥FM,
∴△DHG∽△DMF,
∴ ,
,
即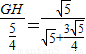 ,
,
∴GH= .
.
点评:此题考查了相似三角形的判定与性质、全等三角形的判定与性质、等腰直角三角形的判定与性质以及勾股定理等知识.此题综合性较强,难度较大,注意掌握数形结合思想与方程思想的应用.
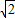 DE;
DE;(2)易证得△DBE∽△CFE,根据相似三角形的对应边成比例,可得DE=
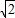 EC,设EC=x,则DE=
EC,设EC=x,则DE=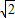 x,由(1)结论可得:6-x=2x,则可求得DE等线段的长度,又由△ADH≌△CDB,可求得DH与CA的长,然后过F做FM∥AE交CD于点M,由相似三角形的对应边成比例,即可求得GH的长.
x,由(1)结论可得:6-x=2x,则可求得DE等线段的长度,又由△ADH≌△CDB,可求得DH与CA的长,然后过F做FM∥AE交CD于点M,由相似三角形的对应边成比例,即可求得GH的长.解答:
 解:(1)过点D作DN⊥DE交AE于点N.
解:(1)过点D作DN⊥DE交AE于点N.∵CD⊥AD,∠BAC=45°,
∴∠ACD=45°,
∴AD=CD.
∵∠ADN+∠NDC=∠ADC=90°=∠NDC+∠EDC,
∴∠ADN=∠EDC,
∵高线CD与高线AE相交于点H,
∴∠DAH+∠B=90°,∠DCB+∠B=90°,
∴∠DAH=∠DCB,
在△ADN和△CDE中,
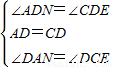 ,
,∴△ADN≌△CDE(ASA),
∴CE=AN,DE=DN,
∴∠DEN=45°,EN=
 DE,
DE,∴AE-EC=AE-AN=EN=
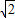 DE;
DE;(2)由(1)可得:∠BED=45°,
∵AE⊥BC,
∴∠AEC=90°,EF平分∠AEC,

∴∠CEF=45°,
∴∠CEF=∠BED,∠CFE=180°-∠CEF-∠ACB=180°-45°-∠ACB,
∵∠BAC=45°,
∴∠B=180°-∠BAC-∠ACB=180°-45°-∠ACB,
∴∠B=∠CFE,
∴△DBE∽△CFE,
∴
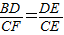 ,
,∵BD=
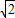 CF,
CF,∴DE=
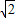 EC,
EC,设EC=x,则DE=
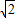 x,
x,由(1)结论可得:6-x=2x,
解得:x=2,
∴EC=2,DE=2
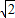 ,
,过D作DK⊥BC于K,
∵∠DEB=45°,
∴DK=EK=
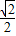 DE=2,
DE=2,∴CK=EK+EC=4,
∴tan∠DCK=
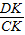 =
= =
= ,CD=
,CD=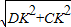 =2
=2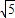 ,
,∴BD=
 CD=
CD=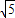 ,BC=5,
,BC=5,∴CF=
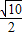 ,
,∵AE∥DK,EK=EC,
∴EH=
 DK=1,CH=
DK=1,CH= CD=
CD=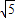 ,
,∴AH=AE-EH=5,
∴AH=BC,
由(1)得:∠DAH=∠DCB,AD=BC,
在△ADH和△CDB中,
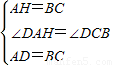 ,
,∴△ADH≌△CDB(SAS),
∴DH=BD=
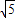 ,CA=
,CA=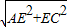 =2
=2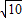 ,
,过F做FM∥AE交CD于点M,
则△CFM∽△CAH,
∴
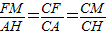 =
= ,
,∴FM=
 ,CM=
,CM=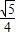 ,MH=
,MH=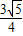 ,
,又∵GH∥FM,
∴△DHG∽△DMF,
∴
 ,
,即
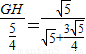 ,
,∴GH=
 .
.点评:此题考查了相似三角形的判定与性质、全等三角形的判定与性质、等腰直角三角形的判定与性质以及勾股定理等知识.此题综合性较强,难度较大,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
相关题目
