题目内容
 如图,AB是圆的直径,AB⊥CD,∠BAD=30°,则∠AEC的度数等于( )
如图,AB是圆的直径,AB⊥CD,∠BAD=30°,则∠AEC的度数等于( )分析:先根据圆周角、弧的关系得出
的度数,再由垂径定理求出
的度数,进而得出
的度数,由圆周角、弧的关系即可得出结论.
 |
| BD |
 |
| BC |
 |
| AC |
解答:解:∵∠BAD=30°,
∴
=60°,
∵AB是圆的直径,AB⊥CD,
∴
=
=60°,
∴
=180°-60°=120°,
∴∠AEC=
=
×120°=60°.
故选C.
∴
 |
| BD |
∵AB是圆的直径,AB⊥CD,
∴
 |
| BC |
 |
| BD |
∴
 |
| AC |
∴∠AEC=
| 1 |
| 2 |
 |
| AC |
| 1 |
| 2 |
故选C.
点评:本题考查的是圆周角定理、垂径定理等知识,熟知圆心角、弧、弦的关系是解答此题的关键.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
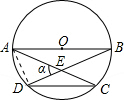 如图,AB是圆的直径,CD是平行于AB的弦,且AC和BD相交于E,∠AED=α,那么△CDE与△ABE的面积之比是( )
如图,AB是圆的直径,CD是平行于AB的弦,且AC和BD相交于E,∠AED=α,那么△CDE与△ABE的面积之比是( )| A、cosα | B、sin2α | C、cos2α | D、1-sinα |
 如图,AB是圆的直径,点C是圆上的一点,且AB=5,BC=3,则sin∠CAB=( )
如图,AB是圆的直径,点C是圆上的一点,且AB=5,BC=3,则sin∠CAB=( ) 的直径,AC是圆
的直径,AC是圆 ,
, .在图中画出弦AD,使AD=1,则
.在图中画出弦AD,使AD=1,则 的度数为 ▲
的度数为 ▲  .
.
