题目内容
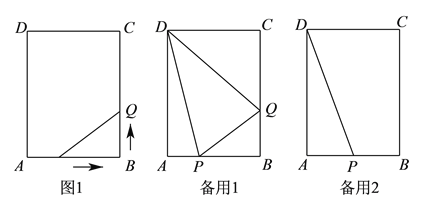
【题目】如图，长方形ABCD的各边与坐标轴都平行，点A，C的坐标分别为(－1，1)，(
，－2
)．
(1)求点B，D的坐标．
(2)一动点P从点A出发，沿长方形的边AB，BC运动至点C停止，运动速度为每秒
个单位长度，设运动时间为t s.
①当t＝1时，求点P的坐标；
②当t＝3时，求三角形PDC的面积．
【答案】(1)B(
，1)，D(－1，－2
)．(2)①(
－1，1)②1＋
【解析】试题分析：(1)、点B的横坐标和点C的相同，纵坐标和点A的相同；点D的横坐标和点A的相同，纵坐标和点C的相同；(2)、①根据t=1得出AP的长度，从而得出点P的坐标；②、首先根据题意得出P点的运动长度，然后求出PC的长度，从而得出三角形的面积．
试题解析：(1)、B(
，1)，D(－1，－2
)．
(2)、①、当t＝1时，AP＝
， ∴点P的坐标是(
－1，1)．
②、当t＝3时，点P运动的路程为3
，
此时PC＝AB＋BC－3
＝(1＋
)＋(1＋2
)－3
＝2，
∴S三角形PDC＝
DC·PC＝
×(1＋
)×2＝1＋
， 即三角形PDC的面积为1＋
．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
