Question

【题目】如图，△ABC内接于⊙O，AB=AC，CO的延长线交AB于点D

（1）求证：AO平分∠BAC；
（2）若BC=6，sin∠BAC= ，求AC和CD的长．

Answer 1

【答案】
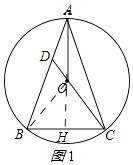
（1）证明：延长AO交BC于H，连接BO，如图1所示：

∵AB=AC，OB=OC，

∴A、O在线段BC的垂直平分线上，

∴AO⊥BC，

又∵AB=AC，

∴AO平分∠BAC；

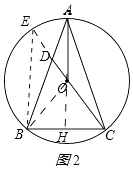
（2）解：延长CD交⊙O于E，连接BE，如图2所示：

则CE是⊙O的直径，

∴∠EBC=90°，BC⊥BE，

∵∠E=∠BAC，

∴sinE=sin∠BAC，

∴ = ，

∴CE= BC=10，

∴BE= =8，OA=OE= CE=5，

∵AH⊥BC，

∴BE∥OA，

∴ ，即 = ，

解得：OD= ，

∴CD=5+ = ，

∵BE∥OA，即BE∥OH，OC=OE，

∴OH是△CEB的中位线，

∴OH= BE=4，CH= BC=3，

∴AH=5+4=9，

在Rt△ACH中，AC= = =3 ．

【解析】（1）圆中常用辅助线是连半径，利用垂直平分线的判定定理可得A、O均在线段BC的垂直平分线上，又由等腰三角形的性质“顶角平分线与高重合”得证；（2）出现三角函数时通常把它放在直角三角形中，因此需延长CD,构造出直径，进而构造出90度的圆周角即直角三角形，可求出直径CE、BE，由BE∥OA可求OD、CD，进而求出AH，利用勾股定理求出AC.
【考点精析】关于本题考查的三角形的外接圆与外心和解直角三角形，需要了解过三角形的三个顶点的圆叫做三角形的外接圆，其圆心叫做三角形的外心；解直角三角形的依据：①边的关系a2+b2=c2；②角的关系：A+B=90°；③边角关系：三角函数的定义．(注意：尽量避免使用中间数据和除法)才能得出正确答案．