题目内容
甲、乙两个工程队分别同时开挖两段河渠,所挖河渠的长度y(m)与挖掘时间x(h)之 间的关系如图所示,请根据图象所提供的信息解答下列问题:
间的关系如图所示,请根据图象所提供的信息解答下列问题:(1)描述乙队在0~6(h)内所挖河渠的长度变化情况;
(2)请你求出:乙队在2≤x≤6的时段内,y与x之间的函数关系式;
(3)当x为何值时,甲队在施工过程中所挖河渠的长度y的值在30和50之间变化?
分析:(1)根据河渠的长度y(m)与挖掘时间x(h)之间的图象关系即可作出描述.
(2)设乙队在2≤x≤6的时段内y与x之间的函数关系式为y=kx+b,根据函数过点(2,30)、(6,50),可求出k与b的值,进而确定关系式.
(3)设甲队在0≤x≤6的时段内y与x之间的函数关系式y=kx,由图可知,函数图象过点(6,60),从而解出k的值,然后根据30≤y≤50可得出x的范围.
(2)设乙队在2≤x≤6的时段内y与x之间的函数关系式为y=kx+b,根据函数过点(2,30)、(6,50),可求出k与b的值,进而确定关系式.
(3)设甲队在0≤x≤6的时段内y与x之间的函数关系式y=kx,由图可知,函数图象过点(6,60),从而解出k的值,然后根据30≤y≤50可得出x的范围.
解答:解:(1)如图,乙队从挖河渠开始至2时,长度由0米增加到30米,从第2时至6时,长度由30米增加到60米.
(2)设乙队在2≤x≤6的时段内y与x之间的函数关系式为y=kx+b,
由图可知,函数图象过点(2,30)、(6,50),
∴
,
解得
,
∴y=5x+20;(7分)
(3)设甲队在0≤x≤6的时段内y与x之间的函数关系式y=kx,
由图可知,函数图象过点(6,60),
∴6k=60,
解得k=10,
∴y=10x.
当y=30时,x=3;
当y=50时,x=5.
∴当3≤x≤5时,甲队所挖河渠的长度y的值在30和50之间变化.
(2)设乙队在2≤x≤6的时段内y与x之间的函数关系式为y=kx+b,
由图可知,函数图象过点(2,30)、(6,50),
∴
|
解得
|
∴y=5x+20;(7分)
(3)设甲队在0≤x≤6的时段内y与x之间的函数关系式y=kx,
由图可知,函数图象过点(6,60),
∴6k=60,
解得k=10,
∴y=10x.
当y=30时,x=3;
当y=50时,x=5.
∴当3≤x≤5时,甲队所挖河渠的长度y的值在30和50之间变化.
点评:此题主要考查学生对函数图象掌握情况及利用待定系数法求一次函数关系式,理解题意是解题的关键.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
甲、乙两个工程队分别同时开挖两段河渠,所挖河渠的长度y(m)与挖掘时间x(h)之间的关系如图所示,请根据图象提供的信息解答下列问题:
(1)甲队在0≤x≤6的时间段内,挖掘速度为每小时 米;乙队在2≤x≤6的时间段内,挖掘速度为每小时 米;请根据乙队在2≤x≤6的时间段内开挖的情况填表:
(2)①请直接写出甲队在0≤x≤6的时间段内,y甲与x之间的关系式;
②根据(1)中的表中规律写出乙队在2≤x≤6的时间段内,y乙与x之间的关系式;
(3)在(1)的基础上,如果甲队施工速度不变,乙队在开挖6小时后,施工速度增加到每小时12米,结果两队同时完成了任务.问甲队从开挖到完工所挖河渠的长度为多少米?

(1)甲队在0≤x≤6的时间段内,挖掘速度为每小时
| 时间(h) | 2 | 3 | 4 | 5 | 6 |
| 乙队开挖河渠(m) | 30 | 50 |
②根据(1)中的表中规律写出乙队在2≤x≤6的时间段内,y乙与x之间的关系式;
(3)在(1)的基础上,如果甲队施工速度不变,乙队在开挖6小时后,施工速度增加到每小时12米,结果两队同时完成了任务.问甲队从开挖到完工所挖河渠的长度为多少米?


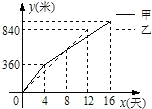 某县在实施“村村通”工程中,决定在A、B两村之间修筑一条公路,甲、乙两个工程队分别从A、B两村同时相向开始修筑.施工期间,乙队因另有任务提前离开,余下的任务由甲队单独完成,直到道路修通.下图是甲、乙两个工程队所修道路的长度y(米)与修筑时间x(天)之间的函数图象,请根据图象所提供的信息,求该公路的总长度.
某县在实施“村村通”工程中,决定在A、B两村之间修筑一条公路,甲、乙两个工程队分别从A、B两村同时相向开始修筑.施工期间,乙队因另有任务提前离开,余下的任务由甲队单独完成,直到道路修通.下图是甲、乙两个工程队所修道路的长度y(米)与修筑时间x(天)之间的函数图象,请根据图象所提供的信息,求该公路的总长度.