题目内容

把三根相同颜色的细绳握在手中，仅露出头和尾，请另一个同学随意选两个头相接，选两个尾相接，放开手后，有两根绳子连成一个环的概率为________．

$\text{[math]}$
分析：列举出所有情况，让放开手后3根绳子恰好连成一个圈的情况数除以总情况数即为所求的概率．
解答：

解：如图所示：据题意分析可得：
假设3根绳子两端分别为：A，B，C，a，b，c；
则连接后的结果为：AB，ab； AB，cb； AB，ac；
AC，ab； AC，ac； AC，bc；
BC，ab；BC，cb；BC，ac；共9种连接方法，
其中有3种能连成一个圈，即：AB，ab；AC，ac；BC，cb
即3条绳子依次首尾相接；
故其概率为 $\text{[math]}$ = $\text{[math]}$ ．
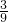故答案为： $\text{[math]}$ ．
点评：此题考查概率的求法：如果一个事件有n种可能，而且这些事件的可能性相同，其中事件A出现m种结果，那么事件A的概率P（A）= $\text{[math]}$ ．