题目内容
在△ABC中,BD平分∠ABC,CD平分△ABC的外角∠ACE,BD、CD交于点D(1)如图①,若∠A=80°,则∠D=
(2)在题(1)的探索中,你发现∠D的大小与∠A有关吗?如果有关,写出你的发现过程;如果没有,请说明理由(借助图①)
(3)如图②,若∠DBC、∠DCE的角平分线BD′、CD′交于点D′,当∠BD′C=30°时,∠A=

分析:(1)因为由角平分线定义和三角形的外角性质及三角形的内角和定理可求出相应的∠D;
(2)有关,角D等于角A的一半,原因是,如图①,因为角ACE为三角形ABC的外角,根据三角形的外角性质可知角ACE等于角A加角ABC,又因为BD为角平分线,根据角平分线定义可知,角ACE等于角A加角DBC的2倍,同理可得角DCE等于角D加角DCE的2倍,CD为角ACE的角平分线,所以角ACE等于角DCE的2倍,综合上面的式子可得出角D与角A的关系;
(3)根据(2)找出的结论可知角D′等于角D的一半,而角D等于角A的一半,所以角A等于角D′的四倍,根据角D′的值即可求出角A的值.
(2)有关,角D等于角A的一半,原因是,如图①,因为角ACE为三角形ABC的外角,根据三角形的外角性质可知角ACE等于角A加角ABC,又因为BD为角平分线,根据角平分线定义可知,角ACE等于角A加角DBC的2倍,同理可得角DCE等于角D加角DCE的2倍,CD为角ACE的角平分线,所以角ACE等于角DCE的2倍,综合上面的式子可得出角D与角A的关系;
(3)根据(2)找出的结论可知角D′等于角D的一半,而角D等于角A的一半,所以角A等于角D′的四倍,根据角D′的值即可求出角A的值.
解答:解:(1)当∠A=80°时,因为∠ACE是△ABC的外角,所以∠ACE=80°+∠ABC,
又因为BD平分∠ABC,所以∠ACE=80°+2∠DBC,
同理∠DCE是△BCD的外角,所以∠DCE=∠D+∠DBC,且∠ACE=2∠DCE,
80°+2∠DBC=2∠DCE=2(∠D+∠DBC)=2∠D+2∠DBC,
所以2∠D=80°,解得∠D=40°,
当∠A=90°时,同理可得∠D=45°;
(2)∠D=
∠A.因为∠ACE是△ABC的外角,所以∠ACE=∠A+∠ABC,又因为BD平分∠ABC,所以∠ACE=∠A+2∠DBC①,
同理∠DCE是△BCD的外角,所以∠DCE=∠D+∠DBC②,且∠ACE=2∠DCE,综合①②可得∠D=
∠A;
(3)由(2)得到的结论可知,∠BD′C=
∠D,∠D=
∠A,所以∠A=4∠BD′C=4×30°=120°.

故答案为:40°;45°;120°.
又因为BD平分∠ABC,所以∠ACE=80°+2∠DBC,
同理∠DCE是△BCD的外角,所以∠DCE=∠D+∠DBC,且∠ACE=2∠DCE,
80°+2∠DBC=2∠DCE=2(∠D+∠DBC)=2∠D+2∠DBC,
所以2∠D=80°,解得∠D=40°,
当∠A=90°时,同理可得∠D=45°;
(2)∠D=
| 1 |
| 2 |
同理∠DCE是△BCD的外角,所以∠DCE=∠D+∠DBC②,且∠ACE=2∠DCE,综合①②可得∠D=
| 1 |
| 2 |
(3)由(2)得到的结论可知,∠BD′C=
| 1 |
| 2 |
| 1 |
| 2 |

故答案为:40°;45°;120°.
点评:此题考查学生灵活运用三角形的外角性质及角平分线的定义解决数学问题的能力,让学生经历特殊到一般的过程,是一道中档题.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
 如图:在△ABC中,∠C=90°,DF⊥AB,垂足为F,DE=BD,CE=FB.
如图:在△ABC中,∠C=90°,DF⊥AB,垂足为F,DE=BD,CE=FB.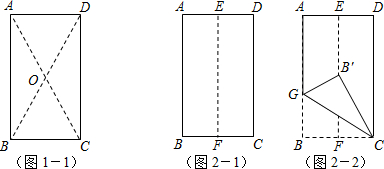
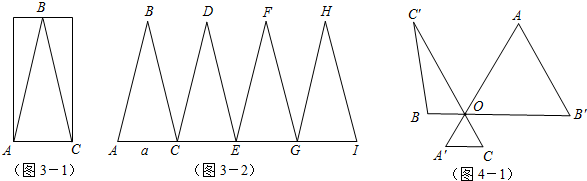
 (2013•平南县二模)如图,在扇形EAB中,半径长AB=10,∠EAB=90°;以AB为直径作半圆O,点D是弧BE上的一个动点,BD与半圆O交于点C,DG⊥AB于点G,DG与AC交于点F,连结OF.
(2013•平南县二模)如图,在扇形EAB中,半径长AB=10,∠EAB=90°;以AB为直径作半圆O,点D是弧BE上的一个动点,BD与半圆O交于点C,DG⊥AB于点G,DG与AC交于点F,连结OF.


 如图:在△ABC中,∠C=90°,DF⊥AB,垂足为F,DE=BD,CE=FB.
如图:在△ABC中,∠C=90°,DF⊥AB,垂足为F,DE=BD,CE=FB.