题目内容
已知：△ABC中，BC=12，∠B=30°，∠C=45°，则△ABC的BC边上高的长为
- A.4（
） - B.36（
） - C.24（）
- D.6（）
D
分析：过点A作AD⊥BC于点D，由已知利用勾股定理可表示出AB，BD，DC的长，已知BC的长，则不难求得AD的长．
解答：
解：过点A作AD⊥BC于点D，
∵AD⊥BC，∠B=30°，∠C=45°，
∴AB=2AD，BD=
AD，AD=DC，
∵BC=12，
∴BD+DC=AD+AD=12，
∴AD=6（-1）．
故选D．
点评：此题主要考查勾股定理及含30度的直角三角形的性质的综合运用．
分析：过点A作AD⊥BC于点D，由已知利用勾股定理可表示出AB，BD，DC的长，已知BC的长，则不难求得AD的长．
解答：
解：过点A作AD⊥BC于点D，∵AD⊥BC，∠B=30°，∠C=45°，
∴AB=2AD，BD=
AD，AD=DC，∵BC=12，
∴BD+DC=
AD+AD=12，∴AD=6（
-1）．故选D．
点评：此题主要考查勾股定理及含30度的直角三角形的性质的综合运用．
练习册系列答案
相关题目
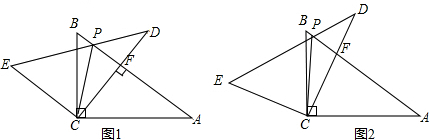
如图所示，已知在△ABC中，AB=AC，∠BAD=β，且AD=AE，求∠EDC．（用β表示）
8、如图，已知在△ABC中，AD垂直平分BC，AC=EC，点B、D、C、E在同一直线上，则下列结论：①AB=AC；②∠CAE=∠E；③AB+BD=DE；④∠BAC=∠ACB．正确的个数有（ ）个．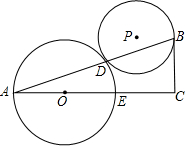
外切于点D，若AC和BC边的长是关于x的方程x2-（AB+4）x+4AB+8=0的两根，且25BC•sinA=9AB，