题目内容
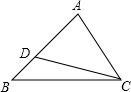 如果,已知:D为△ABC边AB上一点,且AC=
如果,已知:D为△ABC边AB上一点,且AC=| 6 |
分析:过C作CE⊥AB于E,要想求∠BCD的度数,只需求出∠BCE的度数即可.设DE=x,在Rt△DCE中,∠ADC=60°,可求出CE的长;在Rt△AEC中,可根据勾股定理列出等式,从而求出x的值,继而得出BE=CE,求出∠BCE的值.
解答:解:过C作CE⊥AB于E,
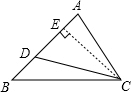
设DE=x,则AE=2-x,
在Rt△DCE中,∠ADC=60°,
∴CE=
x,
在Rt△AEC中,
根据勾股定理得:AE2+CE2=AC2,
∴(2-x)2+(
x)2=(
)2,
解得:x=
,
∴BE=CE=
,
又∠BEC=90°,
∴∠BCE=45°,又∠DCE=90°-∠ADC=90°-60°=30°,
∴∠BCD=∠BCE-∠DCE=15°.

设DE=x,则AE=2-x,
在Rt△DCE中,∠ADC=60°,
∴CE=
| 3 |
在Rt△AEC中,
根据勾股定理得:AE2+CE2=AC2,
∴(2-x)2+(
| 3 |
| 6 |
解得:x=
1+
| ||
| 2 |
∴BE=CE=
3+
| ||
| 2 |
又∠BEC=90°,
∴∠BCE=45°,又∠DCE=90°-∠ADC=90°-60°=30°,
∴∠BCD=∠BCE-∠DCE=15°.
点评:本题考查勾股定理的知识,有一定难度,关键是正确作出辅助线,平时应注意多总结这类题目的解题思路及勾股定理的灵活运用.

练习册系列答案
相关题目

 如果,已知:D为△ABC边AB上一点,且AC=
如果,已知:D为△ABC边AB上一点,且AC= ,AD=2,DB=1,∠ADC=60°,求∠BCD的度数.
,AD=2,DB=1,∠ADC=60°,求∠BCD的度数.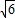 ,AD=2,DB=1,∠ADC=60°,求∠BCD的度数.
,AD=2,DB=1,∠ADC=60°,求∠BCD的度数.