题目内容
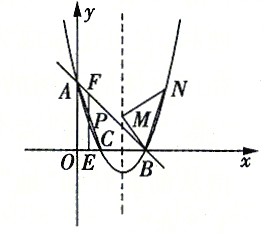
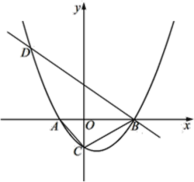
【题目】如图,已知抛物线![]() (
(![]() 为常数,且
为常数,且![]() )与
)与![]() 轴从左至右依次交于A,B两点,与
轴从左至右依次交于A,B两点,与![]() 轴交于点C,经过点B的直线
轴交于点C,经过点B的直线![]() 与抛物线的另一交点为D,点D的横坐标为-4.
与抛物线的另一交点为D,点D的横坐标为-4.
(1)求直线![]() 的函数解析式;
的函数解析式;
(2)求抛物线的函数解析式;
(3)分别求出tan∠ABC和tan∠BAC的值;
(4)在第一象限的抛物线上是否存在点P,使得以A,B,P为顶点的三角形与△ABC相似?若存在,请求出点P的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)tan∠ABC=
;(3)tan∠ABC=![]() ,tan∠BAC=
,tan∠BAC=![]() ;(4)在第一象限的抛物线上存在点P(6,
;(4)在第一象限的抛物线上存在点P(6,![]() ),使得△PAB∽△ABC.
),使得△PAB∽△ABC.
【解析】
(1)根据二次函数交点式可以求出![]() ,
,![]() 的值,从而确定出A、B的坐标,将B点坐标代入一次函数解析式,求出b的值即可解决.
的值,从而确定出A、B的坐标,将B点坐标代入一次函数解析式,求出b的值即可解决.
(2)D点在一次函数的图像上,且知道D点的横坐标,故可以将D点的横坐标代入一次函数解析式,求出D点的坐标,然后将D点的坐标代入二次函数解析式即可求k的值,依次解决.
(3)由图可知,∠ABC和∠BAC分别在Rt△AOC和Rt△BOC中,C为抛物线与y轴的交点,求出C点坐标,分别求两角的正切值即可.
(4)连接PA,过点P作PH垂直![]() 轴于H,根据二次函数解析式,设出P点的坐标,分别表示出PH和AH,分两种情况进行讨论,分别是△PAB∽△ABC和△PAB∽△BAC,根据三角形相似的性质,列出比例式分别计算求解,然后进行判断即可.
轴于H,根据二次函数解析式,设出P点的坐标,分别表示出PH和AH,分两种情况进行讨论,分别是△PAB∽△ABC和△PAB∽△BAC,根据三角形相似的性质,列出比例式分别计算求解,然后进行判断即可.
解:(1)由![]() 解得
解得![]() -2,
-2,![]() 4,
4,
∴A(-2,0),B(4,0),且B点在直线![]() 上,
上,
∴![]() ,解得
,解得![]() ,
,
∴直线BD的函数解析式为![]() .
.
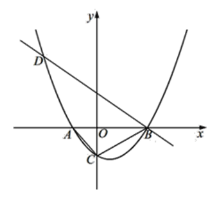
(2)点D在直线BD上,横坐标为-4,故有
![]() ,
,
∴D(-4,![]() ),且点D在抛物线上,故有
),且点D在抛物线上,故有
![]() ,
,
解得![]() ,
,
∴抛物线的函数解析式为![]() .
.
化成一般式为:![]()
(3)由(1)知A(-2,0),B(4,0),所以OA=2,OB=4,
C点是抛物线与![]() 轴的交点,
轴的交点,
将![]() 代入(2)中抛物线的解析式求得
代入(2)中抛物线的解析式求得![]() ,
,
∴C(0,![]() ),
),
∴OC=![]() .
.
在Rt△AOC,Rt△BOC中,有tan∠ABC=![]() ,
,
tan∠BAC=![]() .
.
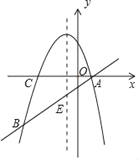
(4)如图,连接PA,过点P作PH垂直![]() 轴于H,
轴于H,
设P(![]() ,
,![]() ),且
),且![]() ,
,
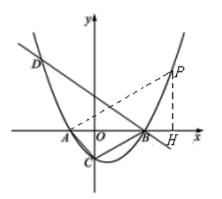
则PH=![]() ,AH=
,AH=![]() +2,分两种情况:
+2,分两种情况:
①若△PAB∽△ABC,
则∠PAB=∠ABC,![]() 同时成立.
同时成立.
由tan∠PAB=tan∠ABC得:![]() ,
,
即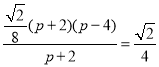 ,
,
解得![]() .
.
∴P(6,![]() ),AH=8,
),AH=8,
∴![]() ,
,
![]() ,
,
由A、B的横坐标求得BA=6,
![]() ,
,![]() ,
,
∴![]() 成立.
成立.
②若△PAB∽△BAC,
则∠PAB=∠BAC,![]() 同时成立.
同时成立.
由tan∠PAB=tan∠BAC得:
![]() ,
,
即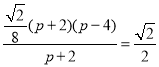 ,
,
解得![]() ,
,
∴P(8,![]() ),AH=10,
),AH=10,
∴![]() ,
,
AC=![]() ,
,
![]() ,
,![]() ,
,
∴![]() .
.
综上,在第一象限的抛物线上存在点P(6,![]() ),使得△PAB∽△ABC.
),使得△PAB∽△ABC.

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案