题目内容
在正六边形ABCDEF中，点P是AF的中点，如果S正六形ABCDEF=12，则△PCD的面积为________．
4
分析：由正六边形的性质可知AF∥CD，利用平行线得△PCD与△FCD的面积相等，圆心O为CF的中点，可知△FCD的面积为△OCD面积的2倍，再由△OCD面积占正六形ABCDEF的
求解．
解答：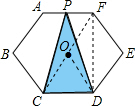
解：如图，连接CF，DF，OD，
∵AF∥CD，
∴S△PCD=S△FCD，
又∵点O为CF的中点，
∴S△FCD=2S△OCD，
∵S△OCD=S正六形ABCDEF=×12=2，
∴S△FCD=2S△OCD=4．
故答案为：4．
点评：本题考查了正多边形与圆．关键是根据正六边形的性质得出平行线，将所求三角形的面积进行转移．
分析：由正六边形的性质可知AF∥CD，利用平行线得△PCD与△FCD的面积相等，圆心O为CF的中点，可知△FCD的面积为△OCD面积的2倍，再由△OCD面积占正六形ABCDEF的
求解．解答：
解：如图，连接CF，DF，OD，∵AF∥CD，
∴S△PCD=S△FCD，
又∵点O为CF的中点，
∴S△FCD=2S△OCD，
∵S△OCD=
S正六形ABCDEF=×12=2，∴S△FCD=2S△OCD=4．
故答案为：4．
点评：本题考查了正多边形与圆．关键是根据正六边形的性质得出平行线，将所求三角形的面积进行转移．
练习册系列答案
相关题目
