题目内容
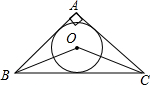 如图,△BAC是直角三角形,其中∠BAC=90°,O是△BAC的内心,则∠BOC=________.
如图,△BAC是直角三角形,其中∠BAC=90°,O是△BAC的内心,则∠BOC=________.
135°
分析:根据三角形内角和定理求出∠ACB+∠ABC,求出∠OBC+∠OCB= (∠ABC+∠ACB),求出∠OBC+∠OCB的度数,根据三角形的内角和定理求出即可.
(∠ABC+∠ACB),求出∠OBC+∠OCB的度数,根据三角形的内角和定理求出即可.
解答:∵∠BAC=90°,
∴∠ABC+∠ACB=180°-90°=90°,
∵点O是△ABC的内心,
∴∠OBC= ∠ABC,∠OCB=
∠ABC,∠OCB= ∠ACB,
∠ACB,
∴∠OBC+∠OCB= (∠ABC+∠ACB)=
(∠ABC+∠ACB)= ×90°=45°,
×90°=45°,
∴∠BOC=180°-45°=135°.
故答案为:135°.
点评:本题考查了三角形的内角和定理,三角形的内切圆与内心的应用,关键是求出∠OBC+∠OCB的度数,题目比较典型,难度适中.
分析:根据三角形内角和定理求出∠ACB+∠ABC,求出∠OBC+∠OCB=
 (∠ABC+∠ACB),求出∠OBC+∠OCB的度数,根据三角形的内角和定理求出即可.
(∠ABC+∠ACB),求出∠OBC+∠OCB的度数,根据三角形的内角和定理求出即可.解答:∵∠BAC=90°,
∴∠ABC+∠ACB=180°-90°=90°,
∵点O是△ABC的内心,
∴∠OBC=
 ∠ABC,∠OCB=
∠ABC,∠OCB= ∠ACB,
∠ACB,∴∠OBC+∠OCB=
 (∠ABC+∠ACB)=
(∠ABC+∠ACB)= ×90°=45°,
×90°=45°,∴∠BOC=180°-45°=135°.
故答案为:135°.
点评:本题考查了三角形的内角和定理,三角形的内切圆与内心的应用,关键是求出∠OBC+∠OCB的度数,题目比较典型,难度适中.

练习册系列答案
相关题目
 (2013•盐城)实践操作
(2013•盐城)实践操作 如图,△BAC是直角三角形,其中∠BAC=90°,O是△BAC的内心,则∠BOC=
如图,△BAC是直角三角形,其中∠BAC=90°,O是△BAC的内心,则∠BOC= 如图,△ABC是直角三角形,∠BAC=90°,AD、AE分别是△ABC的高和中线,AB=6cm,AC=8cm,BC=10cm.
如图,△ABC是直角三角形,∠BAC=90°,AD、AE分别是△ABC的高和中线,AB=6cm,AC=8cm,BC=10cm.