题目内容
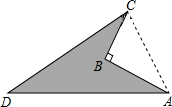 如图阴影部分所示,是一个机器零件的平面示意图,现测得AB=4cm,BC=3cm,AC=5cm,CD=12cm,∠ABC=90°,AD=13.求这个机器零件的面积S.
如图阴影部分所示,是一个机器零件的平面示意图,现测得AB=4cm,BC=3cm,AC=5cm,CD=12cm,∠ABC=90°,AD=13.求这个机器零件的面积S.分析:根据AB=4cm,BC=3cm,∠ABC=90°,∠DCA=90°得出AC的长,进而得出∠ACD=90°,即可得出机器零件的面积.
解答: 解:∵AB=4cm.BC=3cm,∠ABC=90°,
解:∵AB=4cm.BC=3cm,∠ABC=90°,
∴AC=5cm,
∵AC2+CD2=25+144,AD2=169,
∴AC2+CD2=AD2,
∴∠ACD=90°,
所以这个机器零件的面积S=S△ACD-S△ABC=
×5×12-
×3×4=30-6=24.
 解:∵AB=4cm.BC=3cm,∠ABC=90°,
解:∵AB=4cm.BC=3cm,∠ABC=90°,∴AC=5cm,
∵AC2+CD2=25+144,AD2=169,
∴AC2+CD2=AD2,
∴∠ACD=90°,
所以这个机器零件的面积S=S△ACD-S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
点评:此题考查了勾股定理在生活中的应用.善于观察题目的信息是解题以及学好数学的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
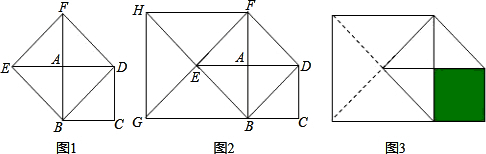
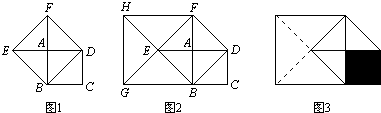
 某学校教学楼前有一个如图阴影部分所示的花坛,其中4个长方形的长和宽分别为a米、b米,它们重叠的部分是边长为c米的小正方形,圆的半径为r米.则花坛(阴影部分)的面积是
某学校教学楼前有一个如图阴影部分所示的花坛,其中4个长方形的长和宽分别为a米、b米,它们重叠的部分是边长为c米的小正方形,圆的半径为r米.则花坛(阴影部分)的面积是 如图阴影部分所示,是一个机器零件的平面示意图,现测得AB=4cm,BC=3cm,AC=5cm,CD=12cm,∠ABC=90°,AD=13.求这个机器零件的面积S.
如图阴影部分所示,是一个机器零件的平面示意图,现测得AB=4cm,BC=3cm,AC=5cm,CD=12cm,∠ABC=90°,AD=13.求这个机器零件的面积S.