题目内容
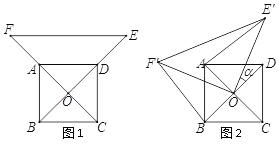
【题目】如图1,已知![]() 为正方形
为正方形![]() 的中心,分别延长
的中心,分别延长![]() 到点
到点![]() ,
, ![]() 到点
到点![]() ,使
,使![]() ,
, ![]() ,连结
,连结![]() ,将△
,将△![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 角得到△
角得到△![]() (如图2).连结
(如图2).连结![]() 、
、![]() .
.
(Ⅰ)探究![]() 与
与![]() 的数量关系,并给予证明;
的数量关系,并给予证明;
(Ⅱ)当![]() ,
, ![]() 时,求:
时,求:
①![]() 的度数;
的度数;
②![]() 的长度.
的长度.
【答案】(1)证明见解析(2)①30°②![]()
【解析】(1)首先证明△AOE′≌△BOF′,根据全等三角形的对应边相等,即可证得;
(2)①延长OA到M,使AM=OA,则OM=OE′.易证△OME′是等边三角形,据此∠AE′O的度数即可求得;②在直角△AOB中,利用三角函数即可求得OB的长,然后在直角△OBF′中利用三角函数求得BF′的长.
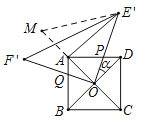
本题解析:如图:
(1)∵正方形ABCD中,OA=OD=OB,
又∵OF=2OA,OE=2OD,
∴OE=OF,则OE′=OF′,
在△AOE′和△BOF′中,
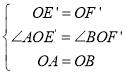
∴△AOE′≌△BOF′
∴AE′=BF′;
(2)①延长OA到M,使AM=OA,则OM=OE′.
∵正方形ABCD中,∠AOD=90°,
∴∠AOE′=90°﹣30°=60°,
∴△OME′是等边三角形,
又∵AM=OA,
∴AE′⊥OM,
则∠E′AO=90°,
∴∠AOE′=90°﹣α=60°,
∴在直角△AOE′中,∠AE′O=90°﹣∠AOE′=30°;
②∵∠AOE′=90°﹣α=60°,∠E′OF′=90°,
∴∠AOF′=30°,
又∵∠AOB=90°,
∴∠BOF′=60°,
又∵等腰直角△AOB中,OB=![]() AB=
AB=![]() ,
,
∴在Rt△ABE'中得到AE'=![]() OA=
OA=![]() ,
,
又BF'=AE'
∴BF′=![]() .
.

练习册系列答案
相关题目