题目内容
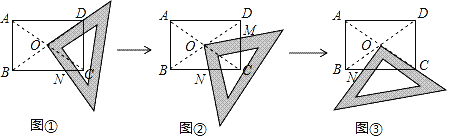
【题目】如图，正方形ABCD的边长为9，将正方形折叠，使顶点D落在BC边上的点E处，折痕为GH．若BE：EC=2：1，则线段CH的长是（ ）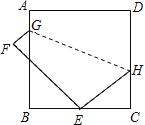
A.3
B.4
C.5
D.6
【答案】B
【解析】解：由题意设CH=xcm，则DH=EH=（9﹣x）cm，
∵BE：EC=2：1，
∴CE= 
BC=3cm
∴在Rt△ECH中，EH2=EC2+CH2 ，
即（9﹣x）2=32+x2 ，
解得：x=4，即CH=4cm．
故选（B）
根据折叠的性质可得DH=EH，在直角△CEH中，若设CH=x，则DH=EH=9﹣x，CE=3cm，可以根据勾股定理列出方程，从而解出CH的长．本题主要考查正方形的性质以及翻折变换，折叠问题其实质是轴对称性质：对应线段相等，对应角相等．找到相应的直角三角形，利用勾股定理求解是解决本题的关键．
练习册系列答案
小学教材完全解读系列答案
相关题目
【题目】一茶叶专卖店经销某种品牌的茶叶，该茶叶的成本价是80元/kg，销售单价不低于120元/kg．且不高于180元/kg，经销一段时间后得到如下数据：
销售单价x（元/kg） | 120 | 130 | … | 180 |
每天销量y（kg） | 100 | 95 | … | 70 |
设y与x的关系是我们所学过的某一种函数关系．
（1）直接写出y与x的函数关系式，并指出自变量x的取值范围；
（2）当销售单价为多少时，销售利润最大？最大利润是多少？
