题目内容
 已知在四边形ABCD中,∠A=120°,∠ABC=90°,AD=3,BC=
已知在四边形ABCD中,∠A=120°,∠ABC=90°,AD=3,BC= ,BD=7
,BD=7
(1)求AB的长;(2)求CD的长.
解:(1)如图,过点D作DE⊥AB,交BA的延长线于点E,
∵∠A=120°,
∴∠EAD=60°,
∴∠EDA=90°-60°=30°,
∵AD=3,
∴AE= AD=
AD= ,
,
在Rt△ADE中,DE= =
= =
=
 ,
,
在Rt△BDE中,BE= =
= =
= ,
,
所以,AB=BE-AE= -
- =5;
=5;
(2)过点D作DF⊥BC于点F,
∵DE⊥AB,∠ABC=90°,
∴四边形BEDF是矩形,
∴BF=DE=
 ,
,
∵BC=3 ,
,
∴CF=BC-BF=3 -
-
 =
=
 ,
,
∴BF=CF,
在△BDF和△CDF中, ,
,
∴△BDF≌△CDF(SAS),
∴CD=BD,
∵BD=7,
∴CD=7.
分析:(1)过点D作DE⊥AB,交BA的延长线于点E,根据∠BAD=120°求出∠EAD=60°,然后求出∠EDA=30°,再根据30°角所对的直角边等于斜边的一半求出AE的长度,再利用勾股定理求出DE的长度,然后在Rt△BDE中,利用勾股定理求出BE的长度,然后根据AB=BE-AE计算即可;
(2)过点D作DF⊥BC于点F,先判定四边形BEDF是矩形,根据矩形的对边相等可得BF的长度,再根据BC的长度求出CF的长度,可得BF=CF,根据“边角边”证明△BDF和△CDF全等,根据全等三角形对应边相等可得CD=BD,从而得解.
点评:本题考查了勾股定理,含30°角的直角三角形,作出辅助线构造出直角三角形是利用勾股定理求解的关键,还考查了全等三角形的判定与性质.
∵∠A=120°,
∴∠EAD=60°,
∴∠EDA=90°-60°=30°,
∵AD=3,
∴AE=
 AD=
AD= ,
,在Rt△ADE中,DE=
 =
= =
=
 ,
,在Rt△BDE中,BE=
 =
= =
= ,
,所以,AB=BE-AE=
 -
- =5;
=5;(2)过点D作DF⊥BC于点F,

∵DE⊥AB,∠ABC=90°,
∴四边形BEDF是矩形,
∴BF=DE=

 ,
,∵BC=3
 ,
,∴CF=BC-BF=3
 -
-
 =
=
 ,
,∴BF=CF,
在△BDF和△CDF中,
 ,
,∴△BDF≌△CDF(SAS),
∴CD=BD,
∵BD=7,
∴CD=7.
分析:(1)过点D作DE⊥AB,交BA的延长线于点E,根据∠BAD=120°求出∠EAD=60°,然后求出∠EDA=30°,再根据30°角所对的直角边等于斜边的一半求出AE的长度,再利用勾股定理求出DE的长度,然后在Rt△BDE中,利用勾股定理求出BE的长度,然后根据AB=BE-AE计算即可;
(2)过点D作DF⊥BC于点F,先判定四边形BEDF是矩形,根据矩形的对边相等可得BF的长度,再根据BC的长度求出CF的长度,可得BF=CF,根据“边角边”证明△BDF和△CDF全等,根据全等三角形对应边相等可得CD=BD,从而得解.
点评:本题考查了勾股定理,含30°角的直角三角形,作出辅助线构造出直角三角形是利用勾股定理求解的关键,还考查了全等三角形的判定与性质.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
 如图,已知在四边形ABCD中,AD=AB,CD=CB,则∠D=∠B,试说明理由.
如图,已知在四边形ABCD中,AD=AB,CD=CB,则∠D=∠B,试说明理由.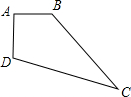 如图,已知在四边形ABCD中,∠A=90°,AB=2cm,
如图,已知在四边形ABCD中,∠A=90°,AB=2cm, 23、如图,已知在四边形ABCD中,∠B=∠D=90度,AE、CF分别是∠DAB及∠DCB的平分线.则AE与FC有什么关系?请说明理由.
23、如图,已知在四边形ABCD中,∠B=∠D=90度,AE、CF分别是∠DAB及∠DCB的平分线.则AE与FC有什么关系?请说明理由. 如图,已知在四边形ABCD中,AC与BD相交于点O,AB⊥AC,CD⊥BD.
如图,已知在四边形ABCD中,AC与BD相交于点O,AB⊥AC,CD⊥BD. 如图,已知在四边形ABCD中,∠ABC=2∠ADC=2a,点E、F分别在CB、CD的延长线上,且EB=AB+AD,∠AEB=∠FAD,猜想线段AE、AF的数量关系,并证明你的猜想.
如图,已知在四边形ABCD中,∠ABC=2∠ADC=2a,点E、F分别在CB、CD的延长线上,且EB=AB+AD,∠AEB=∠FAD,猜想线段AE、AF的数量关系,并证明你的猜想.