题目内容
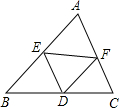 如图,点D、E、F分别是△ABC(AB>AC)各边的中点,下列结论错误的是
如图,点D、E、F分别是△ABC(AB>AC)各边的中点,下列结论错误的是
- A.EF=
 BC
BC - B.EF与AD互相平分
- C.AD平分∠BAC
- D.S△BDE=S△DCF
C
分析:运用三角形中位线定理,得出平行和数量关系,并证明四边形AEDF是平行四边形,再运用平行四边形的性质判断.
解答:∵E、F是ABAC的中点,
∴EF= BC,EF∥BC,
BC,EF∥BC,
故答案A错误;
同理有DE= AC,DE∥AC,DF=
AC,DE∥AC,DF= AB,DF∥AB,
AB,DF∥AB,
∴四边形AEDF是平行四边形,
∴EF与AD互相平分,
故答案A错误;
AD不一定平分∠BAC,
故答案C正确;
∵DE∥AC,DF∥AB,
∴△BDE∽△ABC,△DCF∽△ABC,
∴S△BDE= S△ABC=S△DCF,
S△ABC=S△DCF,
故答案D错误.
故选C.
点评:本题考查了三角形中位线定理、平行四边形的判定和性质、平行线分线段成比例定理的推论、相似三角形的判定和性质.解题的关键是根据中点得出中位线,注意平行四边形的对角线不一定平分对角.
分析:运用三角形中位线定理,得出平行和数量关系,并证明四边形AEDF是平行四边形,再运用平行四边形的性质判断.
解答:∵E、F是ABAC的中点,
∴EF=
 BC,EF∥BC,
BC,EF∥BC,故答案A错误;
同理有DE=
 AC,DE∥AC,DF=
AC,DE∥AC,DF= AB,DF∥AB,
AB,DF∥AB,∴四边形AEDF是平行四边形,
∴EF与AD互相平分,
故答案A错误;
AD不一定平分∠BAC,
故答案C正确;
∵DE∥AC,DF∥AB,
∴△BDE∽△ABC,△DCF∽△ABC,
∴S△BDE=
 S△ABC=S△DCF,
S△ABC=S△DCF,故答案D错误.
故选C.
点评:本题考查了三角形中位线定理、平行四边形的判定和性质、平行线分线段成比例定理的推论、相似三角形的判定和性质.解题的关键是根据中点得出中位线,注意平行四边形的对角线不一定平分对角.

练习册系列答案
相关题目
 如图,点D,E,F分别是△ABC(AB>AC)各边的中点,下列说法中,错误的是( )
如图,点D,E,F分别是△ABC(AB>AC)各边的中点,下列说法中,错误的是( )| A、EF与AD互相平分 | ||
B、EF=
| ||
| C、AD平分∠BAC | ||
| D、△DEF∽△ACB |
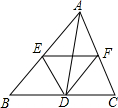 如图,点D,E,F分别是△ABC(AB>AC)各边的中点,下列说法中,错误的是( )
如图,点D,E,F分别是△ABC(AB>AC)各边的中点,下列说法中,错误的是( )| A、AD平分∠BAC | ||
B、EF=
| ||
| C、EF与AD互相平分 | ||
| D、△DFE是△ABC的位似图形 |
 5、如图,点D、E、F分别是△ABC的边AB、BC、AC的中点,连接DE、EF,要使四边形ADEF为正方形,还需增加条件:
5、如图,点D、E、F分别是△ABC的边AB、BC、AC的中点,连接DE、EF,要使四边形ADEF为正方形,还需增加条件: 如图,点D,E,F分别是△ABC的三边AB,AC,BC上的中点,如果△ABC的面积是18cm2,则△DBF的面积是
如图,点D,E,F分别是△ABC的三边AB,AC,BC上的中点,如果△ABC的面积是18cm2,则△DBF的面积是 如图,点D、E、F分别是△ABC三边AB、BC、AC的中点,则△DEF的周长是△ABC周长的( )
如图,点D、E、F分别是△ABC三边AB、BC、AC的中点,则△DEF的周长是△ABC周长的( )