题目内容
13.先阅读下面例题的解题过程,再解决后面的题目.例:已知9-6y-4y2=7,求2y2+3y+7的值.
解:由9-6y-4y2=7,得-6y-4y2=7-9,即6y+4y2=2,所以2y2+3y=1,所以2y2+3y+7=8.
(1)已知代数式14x+5-21x2的值是-2,求3x2-2x+5的值.
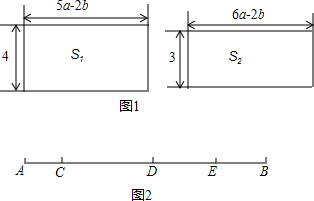
(2)现在请你仿照以上例题的方法,解决下列问题(写出必要的解题过程):若a-b=4,求以下两个长方形的面积的差,即S1-S2的值.
(3)如图,点C、D、E在线段AB上,若2AB+CE=10,计算图中所有线段的和.
分析 (1)根据已知得出3x2-2x=1,再整体代入所求代数式即可;
(2)列出代数式,整理成含有a-b的形式,再将a-b=2代入即可;
(3)将所有线段列出整理为含有2AB+CE=10的形式,再代入即可.
解答 解:(1)∵14x+5-21x2=-2,
∴14x-21x2=-7,
即2x-3x2=-1,
∴3x2-2x=1,
则3x2-2x+5=1+5=6;
(2)两个长方形面积的差是:S1-S2=4(5a-2b)-(6a-2b)=20a-8b-(18a-6b)=2a-2b=2(a-b),
当a-b=4时,S1-S2=2×4=8;
(3)图中线段的和为:(AC+CD+DE+EB)+(AD+DB+CE)+(AE+CE)+AB=4AB+2CE=20.
点评 本题主要考查了代数式求值,整理为已知的形式,整体代入是解答此题的关键.

练习册系列答案
相关题目
18.要说明命题“若a>b,则|a|>|b|”是假命题,能举的一个反例是( )
| A. | a=3,b=2 | B. | a=4,b=-1 | C. | a=1,b=0 | D. | a=1,b=-2 |
3.下列整式的运算中,结果正确的是( )
| A. | 3+x=3x | B. | y+y+y=y3 | C. | 6ab-ab=6 | D. | 3a3b-3ba3=0 |
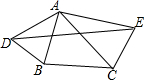 如图,△ABC中,AB=6,AC=8,分别以AB、AC为一边向外作等腰△ADB和等腰△ACE,AD=AB,AE=AC,且∠DAB=∠EAC=x,∠BAC=y(其中2x+y<180°).
如图,△ABC中,AB=6,AC=8,分别以AB、AC为一边向外作等腰△ADB和等腰△ACE,AD=AB,AE=AC,且∠DAB=∠EAC=x,∠BAC=y(其中2x+y<180°).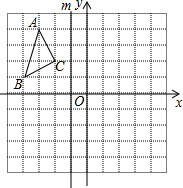 如图所示的正方形网格中,每个小正方形的边长为1,△ABC的三个顶点都在格点上.
如图所示的正方形网格中,每个小正方形的边长为1,△ABC的三个顶点都在格点上.