题目内容
阅读理解:当a>0且x>0时,因为
 ≥0,所以
≥0,所以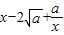 ≥0,从而
≥0,从而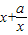 ≥
≥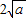 (当
(当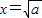 时取等号).设
时取等号).设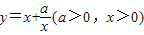 ,由上述结论可知:当
,由上述结论可知:当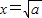 时,y有最小值为
时,y有最小值为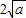 .
.直接应用:已知y1=x(x>0)与
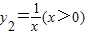 ,则当x=______时,y1+y2取得最小值为______.
,则当x=______时,y1+y2取得最小值为______.变形应用:已知y1=x+1(x>-1)与
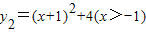 ,求
,求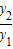 的最小值,并指出取得该最小值时相应的x的值.
的最小值,并指出取得该最小值时相应的x的值.实战演练:
在平面直角坐标系中,点A(-3,0),点B(0,-2).点P是函数y=
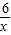 在第一象限内图象上的一个动点,过
在第一象限内图象上的一个动点,过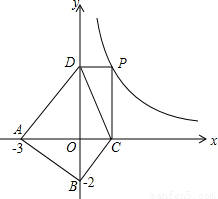 P点作PC垂直于x轴,PD垂直于y轴,垂足分别为点C、D.设点P的横坐标为x,四边形ABCD的面积为S.
P点作PC垂直于x轴,PD垂直于y轴,垂足分别为点C、D.设点P的横坐标为x,四边形ABCD的面积为S.(1)求S和x之间的函数关系;
(2)求S的最小值,判断此时的四边形ABCD是何特殊的四边形,并说明理由.
【答案】分析:直接运用:可以直接套用题意所给的结论,即可得出结果.
变形运用:先得出 的表达式,然后将(x+1)看做一个整体,继而再运用所给结论即可.
的表达式,然后将(x+1)看做一个整体,继而再运用所给结论即可.
实战演练:(1)根据S=S△AOD+S△AOB+S△BOC+S△DOC,进而求出S与x之间的关系求出最值即可;
(2)利用(1)中所求数据,进而得出DC=AD=AB=BC得出答案即可.
解答:解:直接应用:
∵函数y=x+ (a>0,x>0),由上述结论可知:当x=
(a>0,x>0),由上述结论可知:当x= 时,该函数有最小值为2
时,该函数有最小值为2 .
.
∴函数y1=x(x>0)与函数y2= (x>0),则当x=1时,y1+y2取得最小值为2.
(x>0),则当x=1时,y1+y2取得最小值为2.
故答案为:1,2;
变形应用
已知函数y1=x+1(x>-1)与函数y2=(x+1)2+4(x>-1),
则 =
= =(x+1)+
=(x+1)+ 的最小值为:2
的最小值为:2 =4,
=4,
∵当(x+1)+ =4时,
=4时,
整理得出:x2-2x+1=0,
解得:x1=x2=1,
检验:x=1时,x+1=2≠0,
故x=1是原方程的解,
故 的最小值为4,相应的x的值为1;
的最小值为4,相应的x的值为1;
实战演练:
(1)S=S△AOD+S△AOB+S△BOC+S△DOC,
= ×3×
×3× +
+ ×2×3+
×2×3+ ×2×x+
×2×x+ ×x×
×x× ,
,
=x+ +6.
+6.
故x=3时,最大s的最小=2×3+6=12.
(2)当x=3时,CO=3,DO= =2,
=2,
则DC= =
= ,AD=
,AD= =
= ,AB=
,AB= =
= ,BC=
,BC= =
= ,
,
即DC=AD=AB=BC,
故此时的四边形ABCD是菱形.
点评:此题考查了反比例函数的应用及几何不等式的知识和菱形的判定等知识,题目出的比较新颖,解答本题的关键是仔细审题,理解题意所给的结论,达到学以致用的目的.
变形运用:先得出
 的表达式,然后将(x+1)看做一个整体,继而再运用所给结论即可.
的表达式,然后将(x+1)看做一个整体,继而再运用所给结论即可.实战演练:(1)根据S=S△AOD+S△AOB+S△BOC+S△DOC,进而求出S与x之间的关系求出最值即可;
(2)利用(1)中所求数据,进而得出DC=AD=AB=BC得出答案即可.
解答:解:直接应用:
∵函数y=x+
 (a>0,x>0),由上述结论可知:当x=
(a>0,x>0),由上述结论可知:当x= 时,该函数有最小值为2
时,该函数有最小值为2 .
.∴函数y1=x(x>0)与函数y2=
 (x>0),则当x=1时,y1+y2取得最小值为2.
(x>0),则当x=1时,y1+y2取得最小值为2.故答案为:1,2;
变形应用
已知函数y1=x+1(x>-1)与函数y2=(x+1)2+4(x>-1),
则
 =
= =(x+1)+
=(x+1)+ 的最小值为:2
的最小值为:2 =4,
=4,
∵当(x+1)+
 =4时,
=4时,整理得出:x2-2x+1=0,
解得:x1=x2=1,
检验:x=1时,x+1=2≠0,
故x=1是原方程的解,
故
 的最小值为4,相应的x的值为1;
的最小值为4,相应的x的值为1;实战演练:
(1)S=S△AOD+S△AOB+S△BOC+S△DOC,
=
 ×3×
×3× +
+ ×2×3+
×2×3+ ×2×x+
×2×x+ ×x×
×x× ,
,=x+
 +6.
+6.故x=3时,最大s的最小=2×3+6=12.
(2)当x=3时,CO=3,DO=
 =2,
=2,则DC=
 =
= ,AD=
,AD= =
= ,AB=
,AB= =
= ,BC=
,BC= =
= ,
,即DC=AD=AB=BC,
故此时的四边形ABCD是菱形.
点评:此题考查了反比例函数的应用及几何不等式的知识和菱形的判定等知识,题目出的比较新颖,解答本题的关键是仔细审题,理解题意所给的结论,达到学以致用的目的.

练习册系列答案
相关题目

 P点作PC垂直于x轴,PD垂直于y轴,垂足分别为点C、D.设点P的横坐标为x,四边形ABCD的面积为S.
P点作PC垂直于x轴,PD垂直于y轴,垂足分别为点C、D.设点P的横坐标为x,四边形ABCD的面积为S.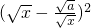 ≥0,所以
≥0,所以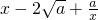 ≥0,从而
≥0,从而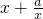 ≥
≥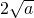 (当
(当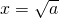 时取等号).设
时取等号).设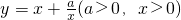 ,由上述结论可知:当
,由上述结论可知:当 ,则当x=______时,y1+y2取得最小值为______.
,则当x=______时,y1+y2取得最小值为______.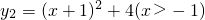 ,求
,求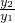 的最小值,并指出取得该最小值时相应的x的值.
的最小值,并指出取得该最小值时相应的x的值. 在第一象限内图象上的一个动点,过
在第一象限内图象上的一个动点,过 P点作PC垂直于x轴,PD垂直于y轴,垂足分别为点C、D.设点P的横坐标为x,四边形ABCD的面积为S.
P点作PC垂直于x轴,PD垂直于y轴,垂足分别为点C、D.设点P的横坐标为x,四边形ABCD的面积为S.