题目内容
如图，在⊙O中，AB是直径，AD是弦，∠ADE = 60°，∠C = 30°．
⑴判断直线CD是否是⊙O的切线，并说明理由；
⑵若CD = 
，求BC的长．
 |
（1）CD是⊙O的切线．
证明：连接OD．
∵∠ADE=60°，∠C=30°，∴∠A=30°．
∵OA=OD，∴∠ODA=∠A=30°．
∴∠ODE=∠ODA+∠ADE=30°+60°=90°，∴OD⊥CD
∴CD是⊙O的切线．
（2）解：在Rt△ODC中，∠ODC=90°， ∠C=30°， CD=
．
∵tanC=
，
∴OD=CD?tanC=×
=3
∴OC=2OD =6．
∵OB=OD=3，∴BC=OC-OB=6-3=3．
练习册系列答案
相关题目
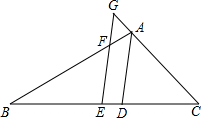如图，在△ABC中，AB＞AC，E为BC边的中点，AD为∠BAC的平分线，过E作AD的平行线，交AB于F，交CA的延长线于G．
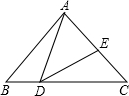如图，在△ABC中，AB=AC，D为BC边上一点，且∠BAD=30°，若AD=DE，∠EDC=33°，则∠DAE的度数为
如图，在△ABC中，AB=AC，D是△ABC内一点，且BD=DC．求证：∠ABD=∠ACD．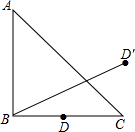
如图，在△ABC中，AB=BC，∠ABC=90°，D是BC的中点，且它关于AC的对称点是D′，BD′=
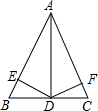如图，在△ABC中，AB=AC，D点是BC的中点，DE⊥AB于E点，DF⊥AC于F点，则图中全等三角形共有