题目内容
已知菱形ABCD的边长为1.∠ADC=60°,等边△AEF两边分别交边DC、CB于点E、F.
(1)特殊发现:如图1,若点E、F分别是边DC、CB的中点.求证:菱形ABCD对角线AC、BD交点O即为等边△AEF的外心;
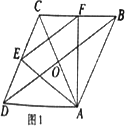
(2)若点E、F始终分别在边DC、CB上移动.记等边△AEF的外心为点P.
①猜想验证:如图2.猜想△AEF的外心P落在哪一直线上,并加以证明;
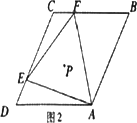
②拓展运用:如图3,当△AEF面积最小时,过点P任作一直线分别交边DA于点M,交边DC的延长线于点N,试判断![]() 是否为定值.若是.请求出该定值;若不是.请说明理由.
是否为定值.若是.请求出该定值;若不是.请说明理由.
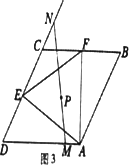
解析:
|
解:(1)证明:如图1,分别连接OE、OF ∵四边形ABCD是菱形 ∴AC⊥BD,BD平分∠ADC.AO=DC=BC ∴∠COD=∠COB=∠AOD=90°. ∠ADO= 又∵E、F分别为DC、CB中点 ∴OE= ∴OE=OF=OA ∴点O即为△AEF的外心.
(2)①猜想:外心P一定落在直线DB上. 证明:如图2,分别连接PE、PA,过点P分别作PI⊥CD于I,PJ⊥AD于J ∴∠PIE=∠PJD=90°,∵∠ADC=60° ∴∠IPJ=360°-∠PIE-∠PJD-∠JDI=120° ∵点P是等边△AEF的外心,∴∠EPA=120°,PE=PA, ∴∠IPJ=∠EPA,∴∠IPE=∠JPA ∴△PIE≌△PJA,∴PI=PJ ∴点P在∠ADC的平分线上,即点P落在直线DB上.
② 当AE⊥DC时.△AEF面积最小, 此时点E、F分别为DC、CB中点. 连接BD、AC交于点P,由(1) 可得点P即为△AEF的外心 解法一:如图3.设MN交BC于点G
设DM=x,DN=y(x≠0.y≠0),则CN= ∵BC∥DA∴△GBP∽△MDP.∴BG=DM=x. ∴ ∵BC∥DA,∴△GBP∽△NDM ∴ ∴ ∴ 其它解法略.
|




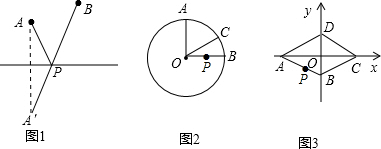
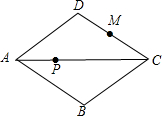 如图,已知菱形ABCD的边长为6,有一内角为60°,M为CD边上的中点,P为对角线AC上的动点,则PD+PM的最小值为
如图,已知菱形ABCD的边长为6,有一内角为60°,M为CD边上的中点,P为对角线AC上的动点,则PD+PM的最小值为 面积.
面积. 如图,已知菱形ABCD的边AB=2cm,它的周长为
如图,已知菱形ABCD的边AB=2cm,它的周长为