题目内容
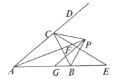
【题目】如图, ![]() 中,
中,![]() ,
,![]() ,
,![]() 为线段
为线段![]() 上一动点(不与点
上一动点(不与点![]() ,
,![]() 重合),连接
重合),连接![]() ,作
,作![]() ,
,![]() 交线段
交线段![]() 于
于![]() .以下四个结论:
.以下四个结论:
①![]() ;
;
②当![]() 为
为![]() 中点时
中点时![]() ;
;
③当![]() 时
时![]() ;
;
④当![]() 为等腰三角形时
为等腰三角形时![]() .
.
其中正确的结论是_________(把你认为正确结论的序号都填上)
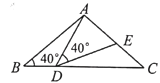
【答案】①②③
【解析】
利用三角形外角的性质可判断①;利用等腰三角形三线合一的性质得到∠ADC=90![]() ,求得∠EDC=50
,求得∠EDC=50![]() ,可判断②;利用三角形内角和定理求得∠DAC=70
,可判断②;利用三角形内角和定理求得∠DAC=70![]() =∠DEA,证得DA=DE,可证得
=∠DEA,证得DA=DE,可证得![]() ,可判断③;当
,可判断③;当![]() 为等腰三角形可分类讨论,可判断④.
为等腰三角形可分类讨论,可判断④.
①∠ADC是![]() 的一个外角,
的一个外角,
∴∠ADC =∠B+∠BAD=40![]() +∠BAD,
+∠BAD,
又∠ADC =40![]() +∠CDE,
+∠CDE,
∴∠CDE=∠BAD,故①正确;
②∵![]() ,
,![]() 为
为![]() 中点,
中点,
∴![]() ,AD⊥BC,
,AD⊥BC,
∴∠ADC=90![]() ,
,
∴∠EDC=90![]() ,
,
∴![]() ,
,
∴DE⊥AC,故②正确;
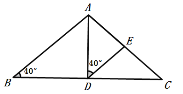
③当![]() 时
时
由①得∠CDE=∠BAD![]() ,
,
在![]() 中,∠DAC=
中,∠DAC=![]() ,
,
在![]() 中,∠AED=
中,∠AED=![]() ,
,
∴DA=ED,
在![]() 和
和![]() 中,
中, ,
,
∴![]() ,
,
∴![]() ,故③正确;
,故③正确;
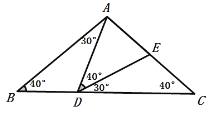
④当AD=AE时,∠AED=∠ADE=40°,
∴∠AED=∠C=40°,
则DE∥BC,不符合题意舍去;
当AD=ED时,∠DAE=∠DEA,
同③,![]() ;
;
当AE=DE时,∠DAE=∠ADE=40°,
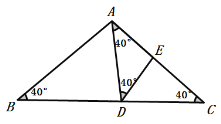
∴∠BAD![]() ,
,
∴当△ADE是等腰三角形时,
∴∠BAD的度数为30°或60°,故④错误;
综上,①②③正确,
故答案为:①②③

 习题精选系列答案
习题精选系列答案【题目】我市某中学开展“社会主义核心价值观”演讲比赛活动,九(1)、九(2)班根据初赛成绩各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如图所示.根据图中数据解决下列问题:

(1)根据图示求出表中的![]() 、
、![]() 、
、![]()
平均数 | 中位数 | 众数 | |
九(1) |
| 85 |
|
九(2) | 85 |
| 100 |
![]() ,
,![]() ,
,![]() .
.
(2)小明同学已经算出了九(2)班复赛成绩的方差:
![]() ,请你求出九(1)班复赛成绩的方差
,请你求出九(1)班复赛成绩的方差![]() ;
;
(3)根据(1)、(2)中计算结果,分析哪个班级的复赛成绩较好?