题目内容
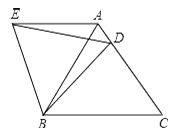
【题目】如图，在
，
，以
为圆心，任意长为半径画弧，分别交
，
于点
，
，再分别以，，为圆心，大于
长为半径画弧，两弧交于点
，作弧线
，交
于点
．已知
，
，则的长为（ ）
A.
B.
C.
D.
【答案】C
【解析】
直接利用基本作图方法得出AE是∠CAB的平分线，进而结合全等三角形的判定与性质得出AC=AD，再利用勾股定理得出AC的长．
过点E作ED⊥AB于点D，由作图方法可得出AE是∠CAB的平分线，
∵EC⊥AC，ED⊥AB，
∴EC=ED=3，
在Rt△ACE和Rt△ADE中，
，
∴Rt△ACE≌Rt△ADE（HL），
∴AC=AD，
∵在Rt△EDB中，DE=3，BE=5，
∴BD=4，
设AC=x，则AB=4+x，
故在Rt△ACB中，
AC2+BC2=AB2，
即x2+82=（x+4）2，
解得：x=6，即AC的长为：6．
故答案为：C．
练习册系列答案
口算能手系列答案
相关题目
