题目内容
【题目】设m,n是任意两个实数,规定m,n两数较大的的数称作这两个数的“绝对最值”,用sec(m,n)表示。例如:sec(-1,-2)=-1,sec(1,2)=2,sec(0,0)=0,参照上面的材料,解答下列问题:
(1)sec(![]() ,3.14)=________,sec(
,3.14)=________,sec(![]() ,
,![]() )=__________;
)=__________;
(2)若sec(-3x-1,x+1)=-3x-1,求x的取值范围;
(3)求函数![]() 与
与![]() 的图象的交点坐标,函数
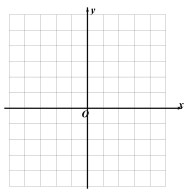
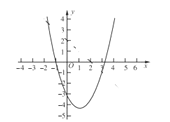
的图象的交点坐标,函数![]() 图象如图所示,请你在图中作出函数
图象如图所示,请你在图中作出函数![]() 的图象,并根据图象直接写出sec(-x+2,
的图象,并根据图象直接写出sec(-x+2, ![]() )的最小值。
)的最小值。
【答案】(1)π,-![]() ;
;
(2)x≤-![]() ;
;
(3)函数y=x2-2x-4与y=-x+2的图象的交点坐标为:(-2,4),(3,-1);
函数y=-x+2的图象见解析;
sec(-x+2, x2-2x-4)的最小值是:-1.
【解析】
(1)根据题目中的规定比较大小直接写出即可;
(2)根据题目中的规定转换成解一元一次不等式即可;
(3)把求交点转换成解一元二次方程即可求出,根据题意画出函数图象即可,观察图象即可sec(-x+2, x2-2x-4)的最小值.
解:(1)∵π>3.14,-![]() <-
<-![]() ,
,
∴sec(π,3.14)=π,sec(-![]() ,-
,-![]() )=-
)=-![]() ;
;
(2)∵sec(-3x-1,x+1)=-3x-1,
∴-3x-1≥x+1,
解得x≤-![]() ;
;
(3)由题意可得二次函数和一次函数的交点可解方程:x2-2x-4=-x+2,解得x1=-2,x2=3,
∴交点坐标为(-2,4),(3,-1);
直线y=-x+2的图象如图所示:
 ;
;
观察函数图象可知:当x=3时,sec(-x+2, x2-2x-4)有最小值为:-1.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目